|
|
Énoncé:
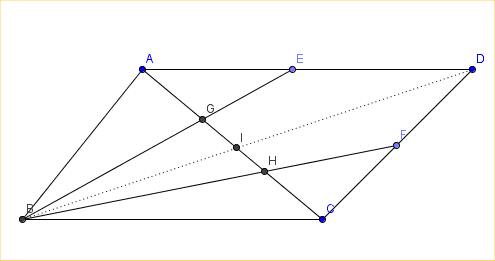
Soit un # ABCD, E et F les milieux des côtés[AD] et [DC]. Démontrer que les segments [BE] et [BF]
coupent la diagonale [AC] en trois segments de même longeur.
Prérequis:
Les propriétés du centre de gravité d'un triangle.
Les diagonales d'un # se coupent en leur milieu.
→ Cliquez ici successivement pour la démonstration par étapes
→ Cliquez ici pour la démonstration entière
→ Cliquez ici pour recommencer
|
Menons la diagonale [BD]. Elle coupe [AC] en I, qui est le milieu de [BD] et [AC]:
G et H sont centres de gravité des triangles ABD et BCD. (en effet le centre de gravité d'un triangle est le point d'intersection des médianes)
On a donc $\vec{AG}=\frac{2}{3}\vec{AI}$ , $\vec{GI}=\frac{1}{3}\vec{AI}$ ,$\vec{IH}=\frac{1}{3}\vec{IC}$ ,$\vec{HC}=\frac{2}{3}\vec{IC}$ (propriétés des centres de gravité)
donc: $\vec{AG}=\frac{1}{3}\vec{AC}$ , $\vec{GI}=\frac{1}{6}\vec{AC}$ ,$\vec{IH}=\frac{1}{6}\vec{IC}$ ,$\vec{HC}=\frac{1}{3}\vec{AC}$ (I milieu de [AC])
donc: $\vec{AG}=\frac{1}{3}\vec{AC}$ , $\vec{GH}=\vec{GI}+\vec{IH}=\frac{1}{3}\vec{AC}$ ,$\vec{HC}=\frac{1}{3}\vec{AC}$
donc: $\vec{AG}=\vec{GH}=\vec{HC}$