|
Énoncé:
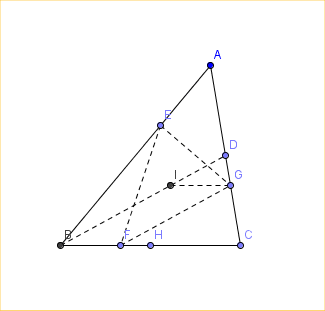
On donne un triangle ABC, E,F et G des points tels que $\vec{AE}=\frac{1}{3}\vec{AB},\vec{BF}=\frac{1}{3}\vec{BC},\vec{CG}=\frac{1}{3}\vec{CA}$
et I son centre de gravité.
Démontrer:
1) I est centre de gravité de EFG.
2) $\vec{FG}=\frac{2}{3}\vec{BD}.$
3) IBFG est un parallélogramme.
Prérequis:
- Définition du parallélogramme: ABCD est un parallélogramme $\iff \vec{AB}=\vec{DC}$
- Définition du centre de gravité : G est centre de gravité du triangle ABC $ \iff \vec{GA} + \vec{GB}+ \vec{GC}$ = $\vec{0}$
- Propriété du centre de gravité : Si G est centre de gravité du triangle ABC et M le milieu de [BC], alors $ \vec{AG} = \frac{2}{3}\vec{AM}$
→ Cliquez ici successivement pour la démonstration par étapes
→ Cliquez ici pour la démonstration entière
→ Cliquez ici pour recommencer
|
1) $\vec{IE}+\vec{IF}+\vec{IG} = \vec{IA}+\vec{AE}+\vec{IB}+\vec{BF}+\vec{IC}+\vec{CG}$ (Chasles)
$ = \vec{IA}+\vec{IB}+\vec{IC}+\frac{1}{3}\vec{AB}+\frac{1}{3}\vec{BC}+\frac{1}{3}\vec{CA}$ (Donnée)
$ = \vec{0}+\frac{1}{3}(\vec{AB}+\vec{BC}+\vec{CA})$ (I centre de gravité de ABC) $= \vec{0}+\frac{1}{3}\vec{0}=\vec{0} $ (Chasles) donc I est centre de gravité de EFG (définition du centre de gravité de EFG)
2) $\vec{BD}=\vec{BF}+\vec{FG}+\vec{GD}= \vec{BF}+\vec{FG}+\vec{GC}+\vec{CA}$ (Chasles)
$\vec{BD}=\frac{1}{3}\vec{BC}+\vec{FG}-\frac{2}{3}\vec{CD}+\vec{CD}$ (D milieu de [AC])$=\frac{1}{3}\vec{BC}+\vec{FG}+\frac{1}{3}\vec{CD} = \vec{FG}+\frac{1}{3}(\vec{BC}+\vec{CD}) = \vec{FG}+\frac{1}{3}\vec{BD}$
3) On sait que $\vec{BI}=\frac{2}{3}\vec{BD}$ (Propriété du centre de gravité), or $\vec{FG}=\frac{2}{3}\vec{BD}$ (point 2)), donc $\vec{BI}=\vec{FG}$ donc IBFG est un parallélogramme


