Énoncé:
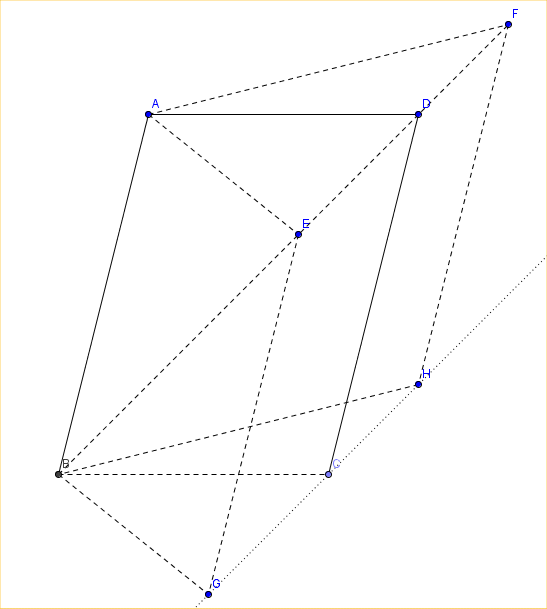
ABCD est un parallélogramme.
On place les points E,F,G et H de telle manière que $\vec{DE}=\frac{1}{3}\vec{DB}$ , $\vec{DF}=\frac{1}{4}\vec{BD}$ et AEGB et AFHB soient des parallélogrammes.
Faire une figure et démontrer que G,C et H sont alignés.

Prérequis:

  1. Définition du parallélogramme: ABCD est un parallélogramme $\iff \vec{AB}=\vec{DC}$
  2. Points alignés: Trois points A,B et C sont alignés $ \iff \vec{AB}$ colinéaire à $\vec{AC}$

→ Cliquez ici successivement pour la démonstration par étapes

→ Cliquez ici pour la démonstration entière

→ Cliquez ici pour recommencer

(1) $\vec{GE}=\vec{BA}=\vec{CD}=\vec{HF}$ (trois parallélogrammes)
(2)$\vec{GC}=\vec{GE}+\vec{ED}+\vec{DC}$ (Chasles)$ = \vec{ED}$ (voir (1))
(3)$\vec{CH}=\vec{CD}+\vec{DF}+\vec{FH}$ (Chasles)$ = \vec{DF}$ (voir (1))
(4)$\vec{DE}=-\frac{1}{3}\vec{DB}$(donnée) = $\frac{1}{3}\vec{BD}$ = $\frac{4}{3}\vec{DF}$ (donnée)
donc $\vec{DE}$ colinéaire à $\vec{BD}$
donc $\vec{GC}$ colinéaire à $\vec{CH}$ (voir (2) et (3))
donc G,C et H alignés