Énoncé:
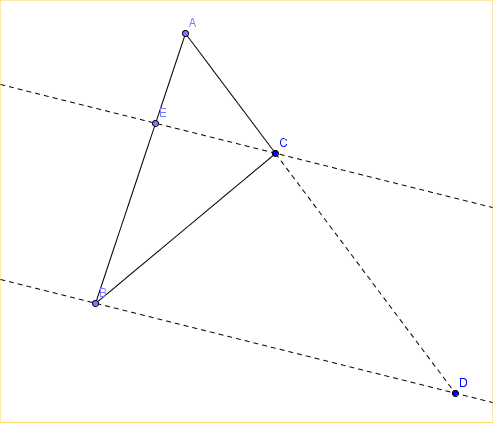
Soit un triangle ABC.
Placer le point E, tel que $\vec{AE}=\frac{1}{3}\vec{AB}.$
Placer le point D, tel que $\vec{AD}=3\vec{AB}.$
Démontrer que les droites (EC) et (DB) sont parallèles.

Prérequis:

  1. Si $A,B \in d$ et $D,C \in d^\prime$ et $\vec{AB}$ colinéaire à $\vec{DC}$ alors $d//d^\prime$
  2. Propriétés des vecteurs.

→ Cliquez ici successivement pour la démonstration par étapes

→ Cliquez ici pour la démonstration entière

→ Cliquez ici pour recommencer

$\vec{DB}=\vec{DA}+\vec{AB}$ (Chasles)
$=3\vec{CA}+3\vec{AE}$ (Données)
$=3(\vec{CA}+\vec{AE})$ (Propriété des vecteurs)
$=3\vec{CE}$ (Chasles)
$\Rightarrow \vec{DB}$ colinéaire à $\vec{CE}$
$\Rightarrow (DB) // DE)$