Énoncé:
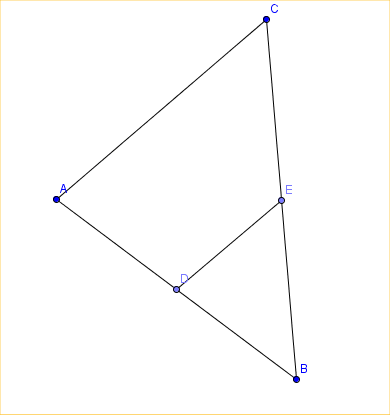
On donne un triangle ABC, D et E étant les milieux de [AB] et [CB].
Démontrez que $2\vec{DE}=\vec{AC}.$

Prérequis:

  1. Définition du milieu : M est milieu de [XY] $\iff \vec{XM}=\vec{MY}$
  2. Relation de Chasles: $ \forall A,B,C : \vec{AB}+\vec{BC}=\vec{AC}$
  3. Opposé: $ \forall A,B: \vec{AB}=-\vec{BA}$

→ Cliquez ici successivement pour la démonstration par étapes

→ Cliquez ici pour la démonstration entière

→ Cliquez ici pour recommencer

$\vec{DE}+\vec{DE}$
$=\vec{DB}+\vec{BE}+\vec{DA}+\vec{AC}+\vec{CE}$ (Chasles)
$=\vec{DB}+\vec{BE}-\vec{AD}+\vec{AC}-\vec{EC}$ (Opposé)
$=\vec{DB}+\vec{BE}-\vec{DB}+\vec{AC}-\vec{BE}$ (Milieux)
$=\vec{AC}}$