Énoncé:
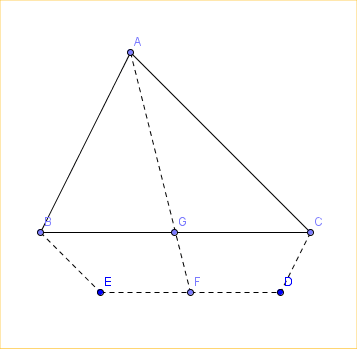
On donne un triangle ABC. Soit G le milieu de [CB] et D et E des points tels que $\vec{CD}=\frac{1}{3}\vec{AB}$ et $\vec{BE}=\frac{1}{3}\vec{}.$ Soit F le milieu de [DE].
Démontrer que A,F et G sont alignés.

Indications:

  1. On commencera la démonstration par $2\vec{AF}.$
  2. Il faudra évidemment utiliser les définitions des milieux G et F.

→ Cliquez ici successivement pour la démonstration par étapes

→ Cliquez ici pour la démonstration entière

→ Cliquez ici pour recommencer

$2\vec{AF}=2\vec{AG}+2\vec{GF}$
$=2\vec{AG}+\vec{GF}+\vec{GF}$
$=2\vec{AG}+\vec{GB}+\vec{BE}+\vec{EF}+\vec{GC}+\vec{CD}+\vec{DF}$ (Chasles)
$=2\vec{AG}+\vec{BE}+\vec{CD}$ (milieux)$
$=2\vec{AG}+\frac{1}{3}(\vec{AC}+\vec{AB})$ (construction)
$=2\vec{AG}+\frac{1}{3}(\vec{AG}+\vec{GC}+\vec{AG}+\vec{GB})$ (Chasles)
$=2\vec{AG}+\frac{1}{3}(\vec{AG}+\vec{AG})$ (milieu)
$=\frac{8}{3}\vec{AG}$
donc: $\vec{AF}= \frac{4}{3}\vec{AG}$
donc: $\vec{AF}$ colinéaire à $\vec{AG}$ et ainsi A,F et G alignés.