Énoncé:
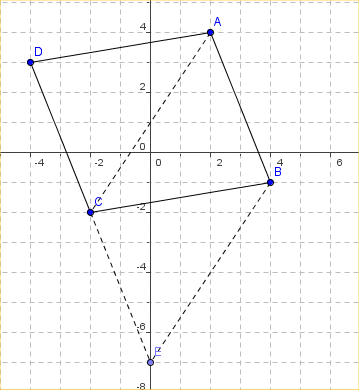
On donne les points A(2,4), B(4,-1), C(-2,-2) et D(-4,3))
1) Démontrer que ABCD est un parallélogramme.
2) Trouver un point E, tel que ABEC soit un parallélogramme.
3) Démontrer que D,C et E sont alignés.

Prérequis:

  1. Définition du parallélogramme: ABCD est un parallélogramme $\iff \vec{AB}=\vec{DC}$
  2. Points alignés: Trois points A,B et C sont alignés $ \iff \vec{AB}$ colinéaire à $\vec{AC}$

→ Cliquez ici successivement pour la démonstration par étapes

→ Cliquez ici pour la démonstration entière

→ Cliquez ici pour recommencer

1) $\vec{AB}={4-2}\choose{-1-4}={2}\choose{-5}$ et $\vec{DC}={-4+2}\choose{3+2}={2}\choose{-5} $
$ \Longrightarrow \vec{AB}$ colinéaire à $\vec{AC}$
$\Longrightarrow$ ABCD est un parallélogramme.
2) $E(x,y)$ est cherché tel que $\vec{CE}=\vec{AB}:$
${x+2}\choose{y+2}={2}\choose{-5}$
$\displaystyle{ \left\{\begin{array}{l l} x+2= & 2 \\ y+2=&-5 \end{array}\right. }$
$\displaystyle{ \left\{\begin{array}{l l} x=& 0 \\ y=&-7 \end{array}\right. }$
$E(0,-7)$
3) $\vec{DC}$ colinéaire à $\vec{DE}?$ ${-2}\choose5$ colinéaire à $4\choose{-10}?$
Est-ce que $(-2)(-10)=5 \cdot 4?$
Oui! Alors $\vec{DC}$ colinéaire à $\vec{DE}$, donc D,C et E sont alignés!