Énoncé:
La focale f de l'appareil photographique vaut 50 mm, Le sapin a une hauteur de 12 m et la distance à l'objectif d est de 15m. La pellicule au fond de l'appareil a les dimensions 24 x 36 mm. Une image complète du sapin sur la pellicule est-elle possible de cette manière?  

Prérequis:

  1. Théorême de Thalès
  2. Calcul avec les proportions

→ solution par étapes

→ aide progressive

→ solution entière

→ effacer tout


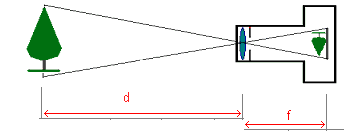
  AF = d; FB = f ; AG = moitié de la hauteur de l'objet ; CB= moitié de la largeur de la pellicule.
  Schématiser pour introduire toutes les données dans une figure "papillon".
  $\frac{AG}{CB}=\frac{AF}{FB}$ (Thalès, figure "papillon")
  $AG=\frac{AF\cdotCB}{FB}=\frac{1500 cm\cdot 1,2 cm}{5 cm}= 360 cm$
Parallélisme:
Le rapport des longueurs:

$\frac{segment}{correspondant}$

est toujours le même!

$\frac{a}{a'}=\frac{b}{b'}=\frac{c}{c'}$
  Considérez la figure "papillon" AGFBCF.
  Calculer AG, la demi-hauteur de l'objet entièrement représentable à l'aide des autres données.
  Hauteur de l'objet = 360 cm x 2 = 720 cm
  Le sapin de hauteur 12 m ne sera pas représenté entièrement sur la pellicule.
  Comparer l'objet entièrement représentable sur pellicule avec le sapin.
3
Parallélisme:
Le rapport des longueurs:

$\frac{segment}{correspondant}$

est toujours le même!

$\frac{a}{a'}=\frac{b}{b'}=\frac{c}{c'}$
4
Deux des rapports

$\frac{segment}{projection}$

égaux:

$\frac{a}{a'}=\frac{b}{b'}(=\frac{c}{c'})$

alors parallélisme!
5
Deux des rapports

$\frac{segment}{projection}$

égaux:

$\frac{a}{a'}=\frac{b}{b'}(=\frac{c}{c'})$

alors parallélisme!
6
Les rapports

$\frac{a}{a'}=\frac{c}{c'}$

égaux

alors parallélisme!
1
Les rapports

$\frac{a}{a'}=\frac{c}{c'}$

égaux

alors parallélisme!
1
h1
1
h1