Retour

Énoncé:

Démontrer que deux cordes de même longueur d'un cercle sont à la même distance du centre.

Prérequis:

  • Théorême de Pythagore:
    Le carré de l'hypothénuse d'un triangle rectangle est égal à la somme des carrés des deux côtés.
  • Triangle isocèle:
    Dans un triangle isocèle, la hauteur relative au sommet est aussi médiane.

→ solution par étapes

→ aide progressive

→ solution entière

→ effacer tout


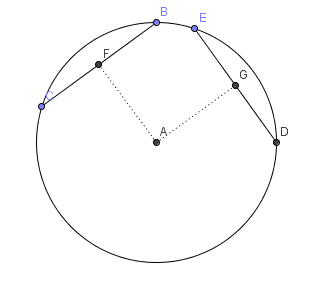
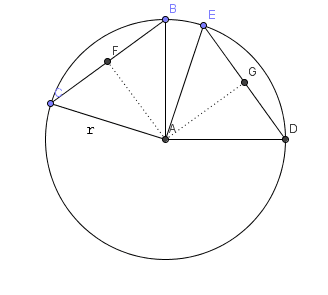  Les deux triangles représentés sont isocèles (rayon!). Alors leurs hauteurs (=distances du centre aux cordes) sont aussi médianes. Donc $FB = \frac{1}{2}BC = \frac{1}{2}DE = EG$ (1)
  Que peut-on dire de FB et EG. Pourquoi? (Utilisez une propriété du triangle isocèle)
  Triangle rect. BFA: $AF^2=AB^2-FB^2=r^2-FB^2$ (2)
  Triangle rect. AGE: $AG^2=AE^2-EG^2=r^2-EG^2$ (3)
  (1) dans (2) et (3): $AF^2 = AG^2$ donc $AF = AG$
c.q.f.d.
  Appliquez le théorême de Pythagore aux triangles BFA et AGE pour comparer AF et AG.