Retour

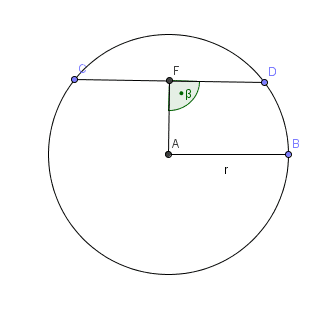
Énoncé:

On donne : $\beta = 90^o$ ; $CD = \frac{3}{2}r$.
Démontrer que $EA = \frac{r}{4}\sqrt{7}$.

Prérequis:

  • Théorême de Pythagore:
    Le carré de l'hypothénuse d'un triangle rectangle est égal à la somme des carrés des deux côtés.
  • Triangle isocèle:
    Dans un triangle isocèle, la hauteur relative au sommet est aussi médiane.

→ solution par étapes

→ aide progressive

→ solution entière

→ effacer tout


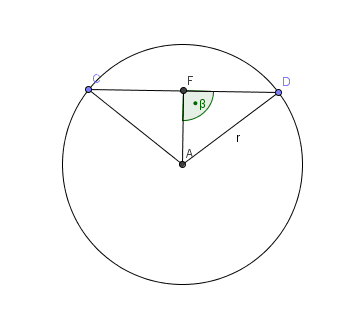  Le triangle CAD est isocèle, car $AD = AC = r$.
  FA est hauteur. Donc aussi médiane.
  Donc FA = $\frac{1}{2}\frac{3}{2}r = \frac{3}{4}r$
  Tracer le triangle CAD. De quel espèce de triangle s'agit-il? Que représente le segment FA? Que vaut FD et pourquoi?
  Triangle rectangle DFA:
   = $FA = \sqrt{AD^2-FD^2 } = \sqrt{r^2-(\frac{3}{4}r)^2 } = \frac{r}{4}\sqrt{7}$
  Appliquez le théorême de Pythagore au triangle rectangle DFA.