Retour

Énoncé:
Démontrer que l'aire du triangle vert est égale à la somme des aires des deux triangles oranges.

Prérequis:

  • Théorême de Pythagore:
    Le carré de l'hypothénuse d'un triangle rectangle est égal à la somme des carrés des deux côtés.

→ solution par étapes

→ aide progressive

→ solution entière

→ effacer tout

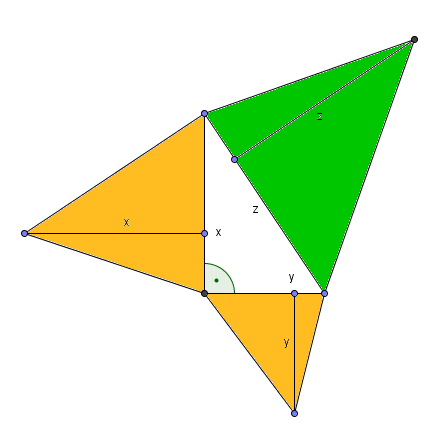
  Aire du triangle vert = $\frac{z\cdotz}{2} = \frac{z^2}{2}$ (1)
  Aire du grand triangle orange = $\frac{x\cdotx}{2} = \frac{x^2}{2}$ (2)
  Aire du petit triangle orange = $\frac{y\cdoty}{2} = \frac{y^2}{2}$ (3)
  Calculer les aires des triangles colorés en fonction de z, x et y.
  $z^2=x^2+y^2$ (4) (théorême de Pythagore)
  (4) dans (1):
  Aire du triangle vert = $\frac{z^2}{2} = \frac{x^2+y^2}{2}$
  = $ \frac{x^2}{2}+\frac{y^2}{2}$
  = Aire du grand triangle orange + Aire du petit triangle orange$
  Écrivez le théorême de Pythagore,introduisez dans (1) et développez!