Retour

Énoncé:
Dans la figure ci-contre les droites (EB) et (IH) sont-elles parallèles? Justifier.

Prérequis:

  • Théorême de Pythagore:
    Le carré de l'hypothénuse d'un triangle rectangle est égal à la somme des carrés des deux côtés.
  • Réciproque du théorême de Pythagore:
    Si le carré du côté h le plus long d'un triangle est égal à la somme des carrés des deux côtés, ce triangle est rectangle avec l'hypothénuse h.

→ solution par étapes

→ aide progressive

→ solution entière

→ effacer tout

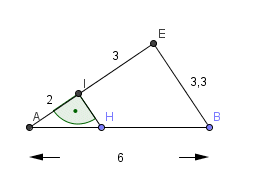
  Triangle $BEA$:
  $AB^2=6^2=36$
  $AE^2+EB^2=5^2+3,3^2=35,89$
  $AB^2\neqAE^2+EB^2$, donc $\hat{AEB}$ n'est pas droit. (Théorême de Pythagore)
  Vérifiez, si le triangle $BEA$ est rectangle.
  Les angles correspondants $\hat{AIH}$ et $\hat{AEB}$ par rapport aux deux droites $(EB)$ et $(IH)$ ne sont pas égaux, donc $(EB)$ n'est pas parallèle à $(IH)$
  Comparez les angles $\hat{AIH}$ et $\hat{AEB}$. Concluez.