Retour

Énoncé:
La figure représentée est un prisme droit à base rectangulaire. Le triangle $BDG$ est-il rectangle?

Prérequis:

  • Théorême de Pythagore:
    Le carré de l'hypothénuse d'un triangle rectangle est égal à la somme des carrés des deux côtés.
  • Réciproque du théorême de Pythagore:
    Si le carré du côté h le plus long d'un triangle est égal à la somme des carrés des deux côtés, ce triangle est rectangle avec l'hypothénuse h.

→ solution par étapes

→ aide progressive

→ solution entière

→ effacer tout

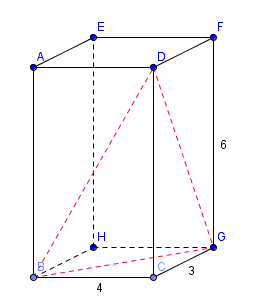
  Triangle rectangle $BCD$:
  $BD^2=BC^2+CD^2=4^2+6^2=52$
  Triangle rectangle(!) $DCG$:
  $DG^2=DC^2+CG^2=6^2+3^2=45$
  Triangle rectangle(!) $BCG$:
  $BG^2=BC^2+CG^2=4^2+3^2=25$
  Calculer $BD^2$, $BG^2$ et $GD^2$ par le théorême de Pythagore direct.
  Triangle $DBG$:
  Carré du côté le plus long = $BD^2=52$
  Somme des carrés des deux autres côtés =
  $BG^2+GD^2 = 70$
  Le triangle $BGD$ n'est donc pas rectangle. (Théorême de Pythagore)
Vérifiez, si dans le triangle $DBG$, le carré du côté le plus long vaut la somme des carrés des deux autres côtés. Conclusion?