Retour

Énoncé:
$ACDE$ est un rectangle. Le triangle $FBD$ est-il rectangle?

Prérequis:

  • Théorême de Pythagore:
    Le carré de l'hypothénuse d'un triangle rectangle est égal à la somme des carrés des deux côtés.
  • Réciproque du théorême de Pythagore:
    Si le carré du côté h le plus long d'un triangle est égal à la somme des carrés des deux côtés, ce triangle est rectangle avec l'hypothénuse h.

→ solution par étapes

→ aide progressive

→ solution entière

→ effacer tout

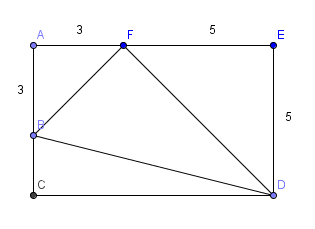
  Triangle $BCD$: $BD^2=BC^2+CD^2=2^2+8^2=68$
  Triangle $ABF$: $BF^2=AB^2+AF^2=3^2+3^2=18$
  Triangle $ABF$: $FD^2=FE^2+ED^2=5^2+5^2=50$
  Calculer $BD^2$, $DF^2$ et $FB^2$ par le théorême de Pythagore direct.
  Triangle $FBD$: $FB^2=68=50+18=FD^2+FB^2$
  Le triangle $FBD$ est rectangle avec l'hypothénuse $BD$ (réciproque du théorême de Pythagore)
Appliquez la réciproque du théorême de Pythagore au triangle $FBD$