Retour

Énoncé:
Une pyramide est représentée. La base est un carré, les faces sont des triangles équilatéraux. Calculez la diagonale de la base, puis la hauteur de la pyramide.

Prérequis:

  • Le carré de l'hypothénuse d'un triangle rectangle est égal à la somme des carrés des deux côtés.

→ solution par étapes

→ aide progressive

→ solution entière

→ effacer tout

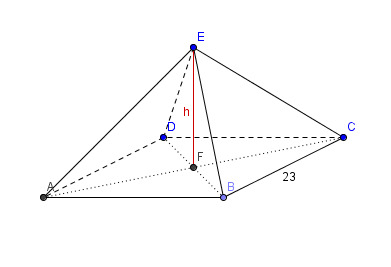
  $DB=\sqrt{AB^2+AD^2}=\sqrt{23^2+23^2}=23\sqrt{2}$
  Appliquez le théorême de Pythagore au triangle rectangle(!) $DAB$
  $EF=\sqrt{EB^2-FB^2}}$
  $=\sqrt{23^2-(\frac{23\sqrt{2}}{2})^2}=\frac{23}{2}\sqrt{2}$
  Appliquez le théorême de Pythagore au triangle rectangle(!) $EFB$.
Hauteur de la pyramide = $\frac{23}{2}\sqrt{2}$
Répondez!