Retour

Énoncé:
$AGEC$ est un carré de côté 6. On découpe les segments égaux $AB=CD=FE=GH=2$. Démontrez que $BHFD$ est un carré et calculez son aire.

Prérequis:

  • Le carré de l'hypothénuse d'un triangle rectangle est égal à la somme des carrés des deux côtés.
  • Somme des angles d'un triangle rectangle.

→ solution par étapes

→ aide progressive

→ solution entière

→ effacer tout

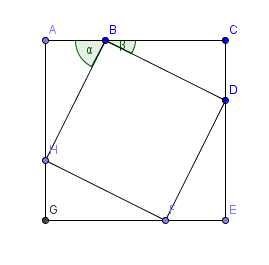
  Les quatre triangles représentés sont isométriques (égaux), car ils ont chacun un angle de $90^0$ compris entre des côtés de longueurs $4$ et $2$.
  Que peut-on dire des quatre triangles de la figure?
  $BH=HF=FD=BD=\sqrt{BC^2+CD^2}=\sqrt{4^2+2^2}=2\sqrt{5}$
  Chercher la longueur d'un côté de la figure $BHFD$
   $\hat{HBD}=180^o-(\alpha+\beta)=180^o-90^o=90^o$ (La somme des angles aigus d'un triangle rectangle vaut $90^o$, triangles isométriques!)
  Que vaut l'angle $\hat{HBD}$?
  $BHFD$ est un carré, car il possède quatre côtés de même longueur et un angle droit.
  Démontrez maintenant que $BHFD$ est un carré.
  Aire du petit carré= $(2\sqrt{5})^2= 20$
  Donnez son aire!