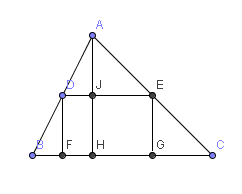
Énoncé: Dans un triangle de $63$ m de base et $54$ m de hauteur, on inscrit un rectangle dont le périmètre vaut $116$ m. Trouver les dimensions de ce rectangle.

  • Équation du premier degré
  • Équations fractionnaires
  • Théorême de Thalès appliqué aux triangles emboîtés.

→ solution par étapes

→ aide progressive

→ solution entière

→ effacer tout

   Soit $x$ la dimension $EG$ du rectangle
   Deuxième dimension du rectangle =
  base du triangle $ADE$ = $\frac{116-2x}{2}=58-x$
   Hauteur du triangle $ADE$ = $AH -JH$ = $54-x$
  Posez: hauteur $EG$ du rectangle = $x$ et exprimez en fonction de $x$ la hauteur et base du triangle $ADE$. .
   Thalès: $\frac{AJ}{AH}=\frac{DE}{BC}$
   $\frac{54-x}{54}=\frac{58-x}{63}$
   Écrivez une égalité de Thalès faisant intervenir la proportionalité des hauteurs et bases des triangles emboîtés $ADE$ et $ABC$.!
  On trouve: $x=30$
  Résolvez!
  1ère dimension du rectangle = $x$ = $30$ m
  2e dimension du rectangle = $58-x$ = $28$ m
  Répondez!