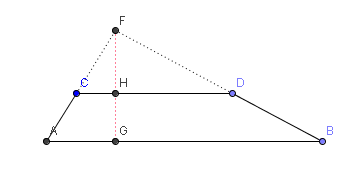
Énoncé: Les bases d'un trapèze mesurent $23$ m et $13$ m, la hauteur $4$ m. Trouver la hauteur du triangle qu'on obtient en prolongeant les côtés non parallèles.

Prérequis:
  • Équation du premier degré
  • Équations fractionnaires
  • Théorême de Thalès appliqué aux triangles emboîtés.

→ solution par étapes

→ aide progressive

→ solution entière

→ effacer tout

   Soit $x$ la hauteur du grand triangle
   Thalès: $\frac{FH}{FG}=\frac{CD}{AB}$
   $\frac{x-4}{x}=\frac{13}{23}$
  Posez: hauteur du grand triangle = $x$ et écrivez une égalité de Thalès faisant intervenir la proportionalité des hauteurs et bases des triangles emboîtés. .
  On trouve: $x=\frac{46}{5}$
   Résolvez!
  Hauteur du triangle obtenu = $\frac{46}{5}$ m
  Répondez!