

|
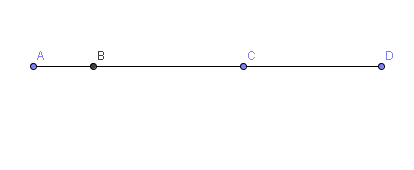
Énoncé: Les points A,B,C et D sont tels que $\frac{BA}{BC}=\frac{DC}{DA}=\frac{2}{5}$. On donne $BD = 4$. Calculez $AC$ .
Prérequis:
|
→ solution par étapes → aide progressive → solution entière → effacer tout |
|
Soit $BA=x$
$\frac{BA}{BC}=\frac{2}{5}$ $BC=\frac{5}{2}x$ (1) |
Posez $AB=x$. Utilisez la première égalité de la donnée pour évaluer $BC$ en fonction de $x$. |
|
$\frac{DC}{DA}=\frac{2}{5}$ $\frac{DB-BC}{DA}=\frac{2}{5}$ $\frac{4-BC}{x+4}=\frac{2}{5}$ $BC=4-\frac{2}{5}(x+4)$ (2)
Utilisez la deuxième égalité de la donnée pour évaluer encore $BC$ en fonction de $x$.
| |
|
$4-\frac{2}{5}(x+4)=\frac{5}{2}x$
|
À l'aide de (1) et (2), formez une équation avec la seule variable $x$
|
|
On trouve $x=\frac{24}{29}$
|
Résolvez!
|
|
$AC=AB+BC=x+4-\frac{2}{5}(x+4)=\frac{84}{29}$
|
Répondez.
|
|
| |
|
| |
|
| |
|
| |
|
|