

|
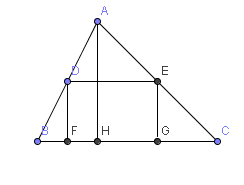
Énoncé: Calculer les dimensions d'un rectangle de périmètre $44$ cm qu'on inscrit dans un triangle de base $BC=30$ cm et de hauteur $AH=20$ cm.
Prérequis:
|
→ solution par étapes → aide progressive → solution entière → effacer tout |
|
Côté $FG$ du rectangle: $x$
Côté $EG$ du rectangle: $\frac{44-2x}{2}=22-x$ Aire du rectangle = $x(22-x)$ |
Désignez le côté "horizontal" du rectangle par $x$, écrivez en fonction de $x$ le côté "vertical" et son aire.
|
|
Hauteur du triangle $ADE = 20-(22-x)=x-2$ Aire du triangle $ADE$= $\frac{x(x-2)}{2}$
Calculez l'aire du triangle $ADE$ en fonction de $x$.
| |
|
Aire du triangle $DBF$= $\frac{BF(x-2)}{2}$
Aire du triangle $EGC$= $\frac{GC(x-2)}{2}$ Aire des deux triangles $DBF$ et $EGC$ = $\frac{BF(x-2)}{2}+\frac{GC(x-2)}{2}=\frac{(BF+GC)(x-2)}{2}=\frac{(30-x)(x-2)}{2}$ |
Calculez l'aire des deux triangles $DBF$ et $EGC$ en fonction de x. Astuce: Que vaut, en fonction de $x$, la somme des hauteurs de ces deux triangles? |
|
$\frac{x(x-2)}{2}+\frac{(30-x)(x-2)}{2}+x(22-x)=\frac{30\cdot20}{2}$
|
Écrivez que la somme des aires des trois triangles et du carré vaut l'aire du triangle entier.
|
|
On trouve $x=\frac{330}{37}$
|
Résolvez, les carrés vont disparaître!
|
|
Côté "horizontal" du rectangle = $\frac{330}{37}$ cm.
Côté "vertical" du rectangle = $22-\frac{330}{37}=\frac{484}{37}$ cm. | Répondez!
|
|
| |
|
| |
|
| |
|
|