Retour

1. Définitions

2. Opérations sur les matrices

   1. Addition, soustraction
   2. Multiplication par un nombre
   3. Transposition
   4. Multiplication des matrices
   5. Inversion des matrices carrées
   6. Déterminant d'une matrice carrée
   
   

3. Application aux systèmes d'équations linéaires

   1. Formulation matricielle
   2. Cas d'une matrice régulière
   3. Cas d'une matrice singulière
   
   

4. Valeurs propres et vecteurs propres

---

I. Définitions

Une matrice n × m est un tableau de nombres à n lignes et m colonnes :

Exemple avec n = 2, m = 3 :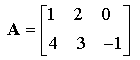

n et m sont les dimensions de la matrice.

Une matrice est symbolisée par une lettre en caractères gras, par exemple A. On note A_ij l'élément situé à l'intersection de la ligne i et de la colonne j (la ligne est toujours nommée en premier).

On note [A_ij] la matrice d'élément général A_ij. On a donc : A = [A_ij]

Si m = 1, la matrice est appelée vecteur (plus précisément vecteur-colonne) :

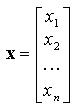
N.B. : Dans ce chapitre, nous utiliserons des lettres majuscules pour les matrices et des lettres minuscules pour les vecteurs, mais ce n'est pas obligatoire.

Si n = m, la matrice est appelée matrice carrée.

Quelques matrices carrées particulières (Exemples avec n = 4)

Matrice unité		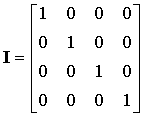Parfois notée In n est la dimension de la matrice (soit I4 dans cet exemple)
Matrice diagonale		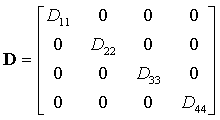notée diag(Dii)
Matrice triangulaire supérieure (Upper triangular matrix, U)
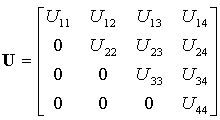Matrice triangulaire inférieure (Lower triangular matrix, L)

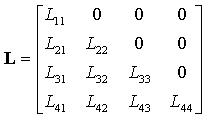Une matrice carrée A est dite symétrique si :

A_ji = A_ij

pour tout i différent de j

---

II. Opérations sur les matrices

---

II.A. Addition, soustraction

L'addition et la soustraction des matrices se font terme à terme. Les matrices doivent avoir les mêmes dimensions :

---

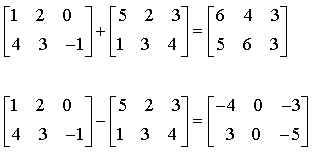
II.B. Multiplication par un nombre

Chaque terme de la matrice est multiplié par le nombre :

---

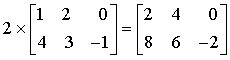
II.C. Transposition

La transposée A^T (aussi notée A') d'une matrice A est la matrice obtenue en échangeant les lignes et les colonnes de A :

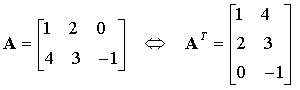
La transposée d'un vecteur-colonne est un vecteur-ligne :

---

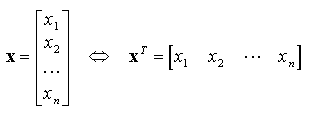
II.D. Multiplication des matrices

Définissons tout d'abord le produit d'un vecteur-ligne x^T par un vecteur-colonne y :

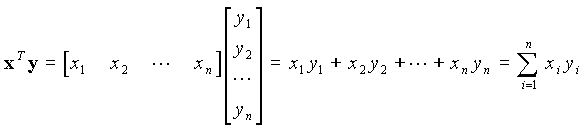
Ce produit est appelé produit scalaire des vecteurs x et y, noté x · y. Les vecteurs doivent avoir la même dimension.

Le produit matriciel s'en déduit : le produit de la matrice A (n × m) par la matrice B (m × p) est la matrice C (n × p) telle que l'élément C_ij est égal au produit scalaire de la ligne i de la matrice A par la colonne j de la matrice B.

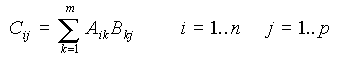
Exemple :

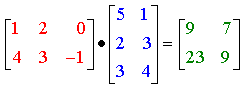
On a en effet, en effectuant les produits ligne par colonne :

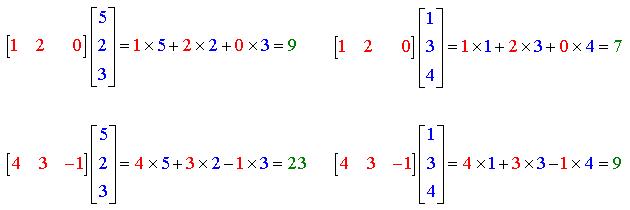
Propriétés :

• Le produit matriciel est :

  • associatif : ABC = (AB)C = A(BC)
  • distributif par rapport à l'addition : A(B + C) = AB + AC
  • non commutatif : AB n'est pas égal à BA en général.
  
  

• La matrice unité I est élément neutre pour la multiplication : AI_m = I_nA = A, si la matrice A est de dimensions n × m.

• Transposée d'un produit : (AB)^T = B^TA^T (Attention au changement d'ordre !).

Quelques produits particuliers :

(x et y sont des vecteurs-colonnes, A est une matrice)

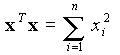	Carré scalaire. Sa racine carrée (xTx)½ est appelée norme du vecteur ( notée )
	Produit extérieur des vecteurs x et y (Matrice d'élément général xiyj) Ne pas confondre avec le produit scalaire.
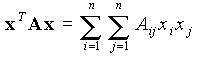	Forme quadratique (si A est symétrique)
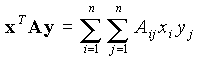	Forme bilinéaire (dite symétrique si A est symétrique)

---

II.E. Inversion des matrices carrées

Une matrice carrée A est dite inversible ou régulière s'il existe une matrice carrée A^-1 (appelée matrice inverse) telle que :

A × A^-1 = A^-1 × A = I

Si A^-1 n'existe pas, la matrice A est dite singulière

Propriétés :

• (A^-1)^-1 = A

• (A^T)^-1 = (A^-1)^T

• (AB)^-1 = B^-1A^-1 (Attention au changement d'ordre !)

• [diag(D_ii)]^-1 = diag(1/D_ii)

• La matrice A est dite orthogonale si A^-1 = A^T

---

II.F. Déterminant d'une matrice carrée

Pour une matrice 2 × 2, on montre que la matrice inverse est donnée par :

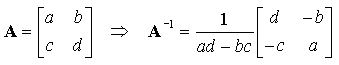
Le nombre ad - bc est appelé déterminant de la matrice A, noté :

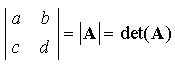
La matrice inverse A^-1 n'existe donc que si det A est différent de zéro.

La matrice A est singulière si det A = 0, régulière dans le cas contraire. Ce résultat se généralise à une matrice de dimension quelconque.

Le déterminant peut se calculer de manière récursive. Par exemple, pour n = 3, on a , en développant par rapport à la première ligne :

Dans ce développement, chaque déterminant d'ordre 2 est appelé mineur du terme qui le précède. Par exemple, le mineur de a est :

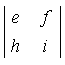
On peut développer le déterminant par rapport à n'importe quelle ligne ou colonne. Pour chaque élément a_ij de la ligne ou colonne choisie :

• le mineur est le déterminant de la sous-matrice obtenue en supprimant la ligne i et la colonne j
• le signe du produit est donné par le tableau :

+ - +
- + -
+ - +

Cette méthode est valable pour un déterminant de taille quelconque. En fait pour n > 3, il vaut mieux utiliser un algorithme spécifique tel que l'algorithme de décomposition LU.

Propriétés des déterminants :

• det(A^T) = det(A)

• det(AB) = det(A) × det(B)

• Le déterminant d'une matrice triangulaire ou diagonale est égal au produit des éléments diagonaux. En particulier, det(I) = 1 (si I est la matrice unité)

• Si A est régulière, det(A^-1) = 1 / det(A)
  puisque det(AA^-1) = det(A) × det(A^-1) = det(I) = 1

• Si A est orthogonale, det(A) = ±1
  puisque det(AA^T) = [det(A)]² = det(I) = 1

---

III. Application aux systèmes d'équations linéaires

---

III.A. Formulation matricielle

Un système de n équations linéaires à n inconnues est de la forme :

a₁₁x₁ + a₁₂x₂ + ... + a_1nx_n = b₁
a₂₁x₁ + a₂₂x₂ + ... + a_2nx_n = b₂
....................................................
a_n1x₁ + a_n2x₂ + ... + a_nnx_n = b_n

où les a_ij sont les coefficients du système, les x_i les inconnues et les b_i les termes constants.

Un tel système peut s'écrire sous forme matricielle :

Ax = b

avec :

---

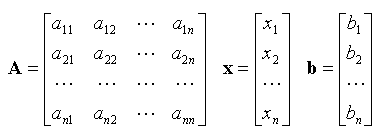
III.B. Cas d'une matrice régulière

Si la matrice A est régulière, on a, en multipliant à gauche par A^-1 :

A^-1Ax = A^-1b

Soit :

x = A^-1b

Exemple :

Soit le système de 2 équations à 2 inconnues :

2x₁ + 3x₂ = 9
x₁ - x₂ = 2

On a successivement :

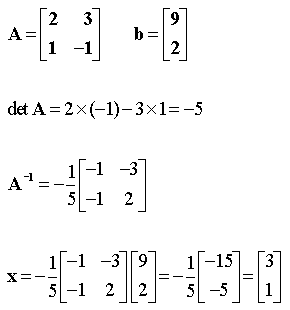
Soit : x₁ = 3, x₂ = 1.

---

III.C. Cas d'une matrice singulière

Lorsque la matrice est singulière, deux cas sont à envisager :

• Système indéterminé

  S'il est possible d'exprimer p équations en fonction des autres, le système admet une infinité de solutions. On peut retenir le vecteur x qui a la plus faible norme.

  L'ensemble des solutions forme un sous-espace de dimension r = n - p dans l'espace de dimension n. Le nombre r est le rang de la matrice.

  Exemple :

  x₁ + x₂ = 3
  2x₁ +2x₂ = 6

  Le déterminant vaut : 1 × 2 - 1 × 2 = 0. La matrice est bien singulière.

  La deuxième équation est égale à la première multipliée par 2. Il n'y a en fait qu'une seule équation : x₁ + x₂ = 3. C'est l'équation d'une droite (espace de dimension 1) dans le plan (x₁, x₂). La matrice est de rang 1.

• Système impossible

  Si les équations ne peuvent pas être exprimées les unes en fonction des autres, le système n'admet aucune solution. On peut cependant calculer un vecteur x tel que la norme du vecteur Ax - b soit minimale (bien que non nulle). Ce vecteur constitue la meilleure approximation de la solution au sens des moindres carrés (régression linéaire).

  Exemple :

  x₁ + x₂ = 3
  2x₁ +2x₂ = 8

  La deuxième équation divisée par 2 donnerait x₁ + x₂ = 4, ce qui est incompatible avec la première équation. Le système n'a pas de solution.

---

IV. Valeurs propres et vecteurs propres

On dit qu'une matrice carrée A posséde une valeur propre l et un vecteur propre associé v si :

Av = l v

En particulier, une matrice symétrique de taille n possède n valeurs propres réelles.

• Exemple : dans le plan xOy rapporté au repére orthonormé (i, j) on considére la symétrie S par rapport é Ox.

  Le vecteur unitaire i est invariant :

  $((1),(0))\rightarrow((1),(0))$

  Le vecteur unitaire j est changé en son opposé :

  S (j) = - j

  $((0),(1))\rightarrow((0),(-1))$

  La matrice S associée à la symétrie est telle que chaque colonne contient les composantes de l'image du vecteur unitaire correspondant :

  S = $[[1,0],[0,-1]]$

  Le vecteur i est un vecteur propre de la matrice S avec la valeur propre associée 1 :

  S i = 1 × i

  Le vecteur j est un vecteur propre de la matrice S avec la valeur propre associée (-1) :

  S j = (- 1) × j

  Note : Tout multiple d'un vecteur propre est également vecteur propre avec la méme valeur propre associée. Les vecteurs propres ne sont donc définis qu'à un coefficient prés.

---