1) Calculer le moment d'inertie par rapport à l'axe $x$ de la surface limitée par la courbe $y^2=x^3$ et de la droite $y=x$ a) en intégrant d'abord par rapport à $y$ b) en intégrant d'abord par rapport à $x$.
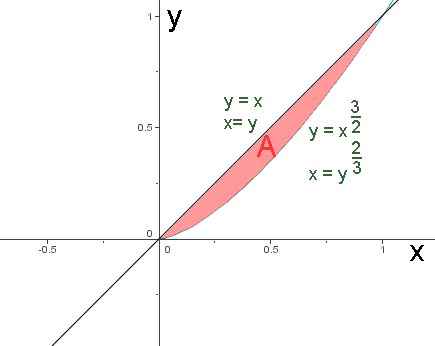
$I_x$ =
$ \int_0^1(\int_{x^{\frac{3}{2}}}^x y^2dy)dx$
= $\int_0^1({\frac{x^3}{3}-\frac{x^\frac{9}{2}}{3})dx
=$\frac{1}{44}$
b)
$I_x$ =
$ \int_0^1(\int_y^{y^{\frac{2}{3}}}y^2dx)dy$
= $\int_0^1(y^{\frac{8}{3}}-y^3)dx
=$\frac{1}{44}$
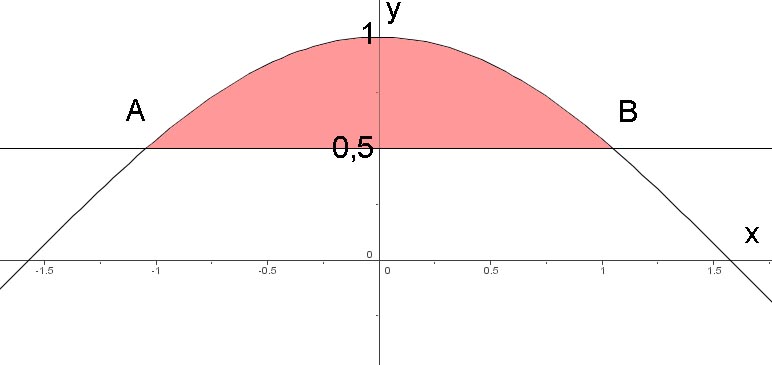
$I_x$ =
$ \int_{-\frac{\pi}{3}}^{\frac{\pi}{3}}(\int_{\frac{1}{2}}^{cosx}y^2dy)dx$
= $ \int_{-\frac{\pi}{3}}^{\frac{\pi}{3}}(\frac{cos^3x}{3}-\frac{1}{24})dx$
=$\frac{1}{3} [(sinx-\frac{sin^3x}{3}-\frac{1}{8}x]_{-\frac{\pi}{3}}^{\frac{\pi}{3}}$
= $ \frac{9\sqrt{3}-\pi}{30}$