Rappel: Rotation
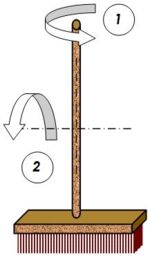
À même vitesse de rotation angulaire ($\omega$ = angle en radians balayé par seconde = $\frac{\theta}{t} $), le mouvement 1 est plus facile que le mouvement 2. Cela vient du fait que dans le mouvement 1, les masses qui tournent sont plus près de l'axe de rotation. Le moment d'inertie est une grandeur introduite pour mesurer la résistance à la rotation.
Énergie cinétique d'un système formé de plusieurs masses de même masse volumique $\rho$ tournant à vitesse angulaire $\omega$ constante autour d'un axe
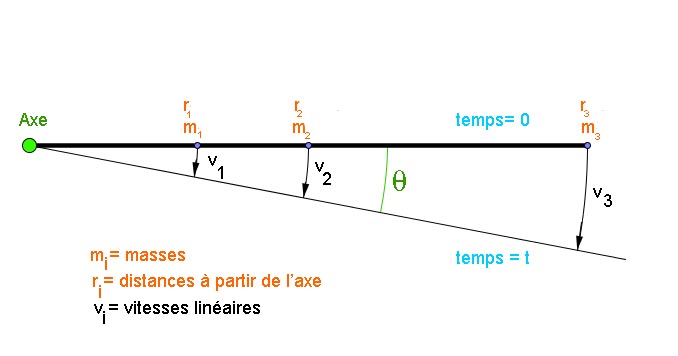
Dans l'exemple représenté, nous pouvons écrire (la barre est supposée de masse négligeable):
Vitesse angulaire = $\omega$ = $\frac{\theta}{t}$
$m_1$ = Masse de 1 = Volume de 1 $\cdot$ masse volumique = $V_1\cdot\rho$
$m_2$ = Masse de 2 = Volume de 2 $\cdot$ masse volumique = $V_2\cdot\rho$
$m_3$ = Masse de 3 = Volume de 3 $\cdot$ masse volumique = $V_3\cdot\rho$
Longueur de l'arc 1 = Mesure en radians de l'arc 1$\cdot$ rayon de l'arc 1 = $\theta\cdot\rho_1$
Longueur de l'arc 2 = Mesure en radians de l'arc 2$\cdot$ rayon de l'arc 2 = $\theta\cdot\rho_2$
Longueur de l'arc 3 = Mesure en radians de l'arc 3$\cdot$ rayon de l'arc 3 = $\theta\cdot\rho_3$
$v_1$ = Vitesse linéaire de 1 = Longueur de l'arc 1/ temps = Vitesse angulaire $\cdot$ rayon de l'arc 1 = $\omega\cdot r_1$
$v_2$ = Vitesse linéaire de 2 = Longueur de l'arc 2/ temps = Vitesse angulaire $\cdot$ rayon de l'arc 2 = $\omega\cdot r_2$
$v_3$ = Vitesse linéaire de 3 = Longueur de l'arc 3/ temps = Vitesse angulaire $\cdot$ rayon de l'arc 3 = $\omega\cdot r_3$
Énergie cinétique de 1 = $\frac{m_1v_1^2}{2}$ = $\frac{m_1\omega^2r_1^2}{2}$
Énergie cinétique de 2 = $\frac{m_2v_2^2}{2}$ = $\frac{m_2\omega^2r_2^2}{2}$
Énergie cinétique de 3 = $\frac{m_3v_3^2}{2}$ = $\frac{m_3\omega^2r_3^2}{2}
Énergie cinétique totale = Énergie cinétique de 1 + Énergie cinétique de 2 + Énergie cinétique de 3
= $\frac{\omega^2}{2}(m_1 r_1^2 + m_2 r_2^2 + m_3 r_3^2$)
= $\frac{\omega^2}{2}(\rho(V_1 r_1^2 + V_2 r_2^2 + V_3 r_3^2)$
= $\frac{\omega^2}{2}\cdot I $, avec $I$ = Moment d'inertie = $\rho(V_1 r_1^2 + V_2 r_2^2 + V_3 r_3^2)$
Moment d'inertie d'un solide de masse volumique $\rho$ par rapport à l'axe [Oz)
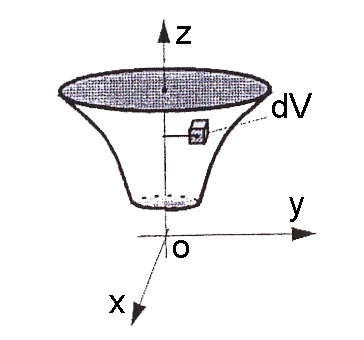
D'après ce qui précède, on a:
En coordonnées cylindriques $dV = r dzdrd\theta$, donc: