Retour

Integrales multiples

Centre de gravité en coordonnées cartésiennes: Exemples de calculs

1) Calculer les coordonnées du centre de gravité de la surface délimitée par la courbe $y=\frac{e^x}{2}$ et les droites $x=1$,$x=3$ et $y=0$.

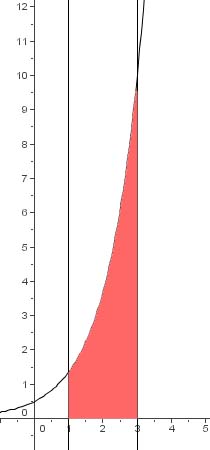
A =
$ \int\int_A dydx$
= $ \int_1^{3}(\int_0^{\frac{e^x}{2}} dy)dx$
= $\frac{e^3-e}{2}$
$x_G =\frac{1}{A}\int_1^{3}(\int_0^{\frac{e^x}{2}} x dy)dx$
= $ \frac{1}{A}e^3$
= $\frac{2e^3}{e^3-e}$
$y_G =\frac{1}{A}\int_1^{3}(\int_0^{\frac{e^x}{2}} y dy)dx$
= $ \frac{1}{A}\frac{e^6-e^2}{16$}
= $\frac{e^3+e^2}{8}$

2) Calculer les coordonnées du centre de gravité d'un demi-disque de rayon a.

A =
$ \frac{\pi a^2}{2}$
$x_G =0$ par raisons de symétrie
$y_G =\frac{1}{A}\int_{-a}^{a}(\int_0^{\sqrt{a^2-x^2} y dy)dx$
= $ \frac{1}{A}\frac{2a^3}{3}$
= $\frac{4a}{3\pi}$