Rappel: Centre de gravité et moments


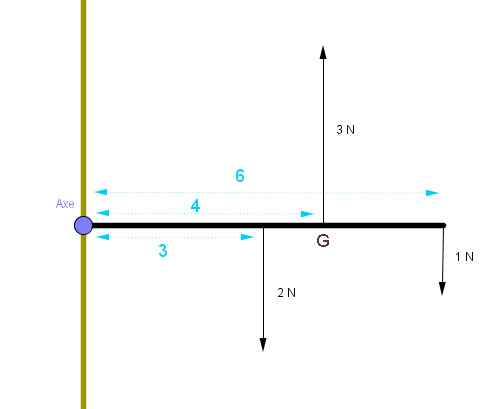
La barre (supposée sans poids) est en équilibre car l y a égalité des moments: $3 \cdot 2 N + 6 \cdot1 N = 4 \cdot 3 N$

Alors on peut dire que le système des deux forces précédentes de $2 N$ et $1 N$ est équivalent à une seule force de 3 N appliquée au point $G$, Ce point est appelé centre de gravité du système:


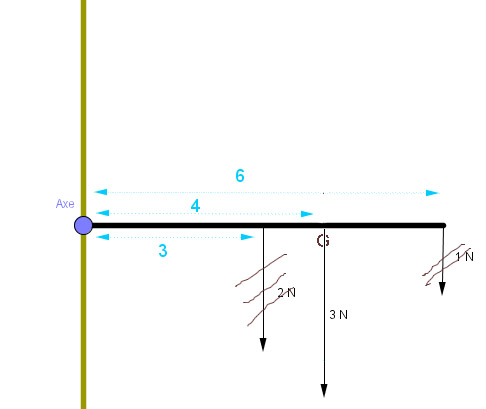
Centre de gravité d'une surface en coordonnées cartésiennes


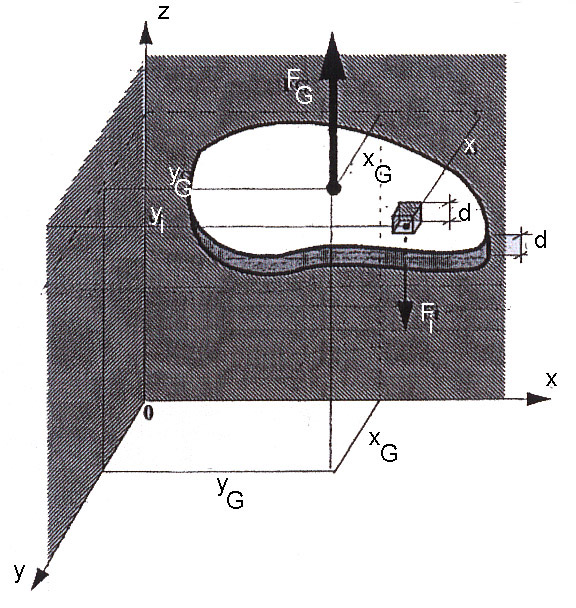
En généralisant les considérations précédentes à 2 dimensions, nous pouvons écrire:

$x_G\cdot F_G = \Sigma_i x_i F_i$

$y_G\cdot F_G = \Sigma_i y_i F_i$

(Comme vu précédemmment, $F_G$ vaut (est opposée) le poids total de l'aire considérée, les i dénotent tous les petits éléments de volume de même épaisseur qui couvrent l'aire entière)

Comme toutes ces forces sont proportionnelles à l'aire dont elles proviennent, on peut écrire:

$y_G\cdot A = \Sigma_i y_i A_i$ et $x_G\cdot A = \Sigma_i x_i A_i$ et

à la limite comme l'élément d'aire "infinitésimal" en coordonnées cartésiennes vaut "dxdy" :

$y_G\cdot A = \int\int_A y dxdy$ et $x_G\cdot A = \int\int_A x dxdy$

ce qui donne les coordonnées $x_G$ et $y_G$ du centre de gravité $G$

Centre de gravité d'une surface en coordonnées polaires


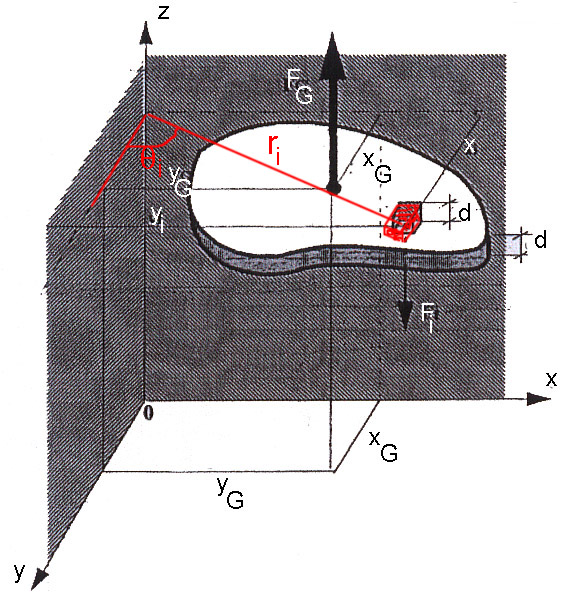
Les formules de transformation en coordonnées polaires (voir) nous donnent:

$y = rsin\theta$, $x = rcos\theta$ et pour l'élément de volume: $rdrd\theta$ , donc:

$y_G\cdot A = \int\int_A rsin\theta r drd\theta$ = $\int\int_A r^2sin\theta drd\theta$ et $x_G\cdot A = \int\int_A rcos\theta r drd\theta$ = $\int\int_A r^2cos\thetadrd\theta$

ce qui donne encore les coordonnées $x_G$ et $y_G$ du centre de gravité $G$