Passage d'un anneau de coordonnées cartésiennes à polaires
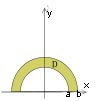
Considérons $\{(x,y) | 4 = x² + y² = 9, y = 0\}$, soit une demi-couronne de rayon extérieur 3 et de rayon intérieur 2 (voir dessin), limitée aux $y$ positifs ; on voit que $\theta$ varie de 0 à $\pi$ et $r$ de 2 à 3. Par conséquent, le domaine transformé en coordonnées polaires est le rectangle $\{(r,\theta) | 2 < r < 3, 0 < \theta < p\}.
Soit $f(x,y) = x$ à intégrer sur ce domaine
 ;
;
puis appliquons la formule pour l'intégration :
 .
.
Enfin :
![\int_0^\pi\mathrm d\theta\int_2^3 r^2\cos\theta\;\mathrm dr = \int_0^\pi\cos\theta\;\mathrm d\theta \left[ \frac{r^3}{3}\right]_2^3 = [\sin\theta]_0^\pi \left(9 - \frac{8}{3}\right) = 0](http://upload.wikimedia.org/math/2/5/f/25fa916ede8aeeabcec98b913980bc2f.png) .
.
Coordonnées cartésiennes vers cylindriques

Il est conseillé d'utiliser cette méthode dans les cas de domaines cylindriques, coniques, ou tout du moins de régions pour lesquelles il est commode tant de délimiter l'intervalle des z que de transformer la base circulaire et la fonction.
Soit f(x,y,z) = x2 + y2 + z à intégrer sur le cylindre {{math|D = { (x,y,z) | x² + y² = 9, -5 = z = 5 }}}. La transformation de D en coordonnées cylindriques est la suivante :
tandis que la fonction devient
- $f(r,\theta,z) = r^2 + z$
Appliquons la formule :
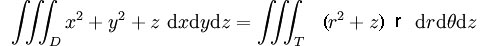 ;
;
En développant :
![\int_{-5}^5 \mathrm{d}z \int_0^{2 \pi} \mathrm{d} \theta\int_0^3 r^3 + r z\; \mathrm{d}r = 2 \pi \int_{-5}^5 \left[ \frac{r^4}{4} + \frac{r^2 z}{2} \right]_0^3 \mathrm{d}z](http://upload.wikimedia.org/math/f/b/b/fbb44f4b2278a27adc9e3eaa1ee6788b.png)
 .
.
Coordonnées cartésiennes vers sphériques (on posera: $\rho = r$)
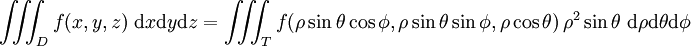
Il est conseillé d'utiliser cette méthode dans le cas de domaines sphériques et de fonctions facilement simplifiables à l'aide des identités trigonométriques étendues à R³ (voir l'exemple suivant) ; dans les autres cas il est souvent conseillé de recourir au passage en coordonnées cylindriques, comme nous le verrons ci-après.
Soit $f(x,y,z) = x^2 + y^2 + z^2$ à intégrer sur le domaine $\{(x,y,z) | x² + y² + z² = 16\}$ (sphère de rayon 4 centrée à l'origine). La transformation de la fonction est très simple:
 ,
,
tandis le domaine reformulé en coordonnées sphériques est le suivant:
 .
.
Appliquons donc la formule pour l'intégration :
 ;
;
développons :
![\iiint_T \rho^4\sin\theta \;\mathrm{d}\rho\mathrm{d}\theta\mathrm{d}\phi =
\int_0^\pi \sin\theta\mathrm{d}\theta \int_0^4 \rho^4\mathrm{d}\rho \int_0^{2\pi} \mathrm{d} \phi =
2 \pi \int_0^\pi \sin \theta\left[ \frac{\rho^5}{5}\right]_0^4 \;\mathrm{d} \theta](http://upload.wikimedia.org/math/8/6/a/86ae280b2f55a4e2abe6c1882828cc0d.png)
![= 2 \pi \left[ \frac{\rho^5}{5} \right]_0^4 \;[- \cos \theta ]_0^\pi = 4 \pi \cdot \frac{1024}{5} = \frac{4096 \pi}{5}](http://upload.wikimedia.org/math/9/f/a/9faf56f7b7e26565ba6e75fa4940e79b.png) .
.