Rappel


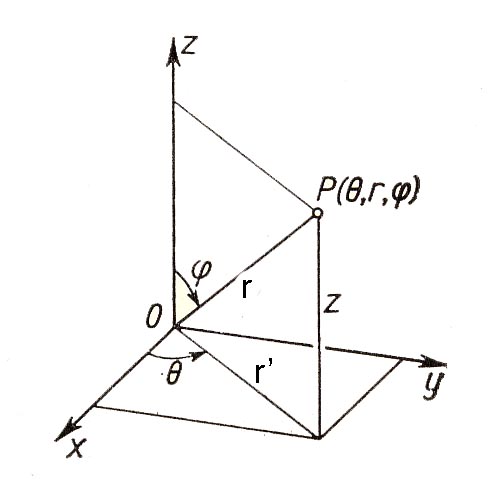
Un point $P(x,y,z)$ en coordonnées cartésiennes possède les coordonnées polaires sphériques $P(\theta,r,\phi)$ avec

$x = rsin\phicos\theta$, $y = rsin\phisin\theta$ et $z = rcos\phi$

(En effet, $r'=rsin\phi$)

dS et dV


L'élément "infinitésimal" d'aire en coordonnées polaires vaut:

$dS = rdrd\theta$

L'élément "infinitésimal" de volume en coordonnées polaires cylindriques vaut:

$dV = r^2sin\phidrd\thetad\phi$

( En effet: $dV = MN'\cdot MN = rsin\phid\theta\cdot rd\phidr$)

Volumes

Connaissant l'équation de la surface $r = f(\theta,\phi)$ on calcule le volume inclus dans cette surface, et balayé par un rayon centré sur l'origine se déplaçant de $\theta1$ à $\theta2$ dans le plan xy à partir de [Ox) et dans le plan vertical de $\phi1$ à $\phi2$ à partir de [Oy), de la manière suivante:

$V = \int\int\int_VdV = \int_{\theta1}^{\theta2}\int_{\phi1}^{\phi2}\int_{0}^{f(\theta,\phi)}r^2sin\phidrd\phid\theta = \int_{\theta1}^{\theta2}[\int_{\phi1}^{\phi2}(\int_{0}^{f(\theta,\phi)}r^2sin\phidr]d\phi)d\theta

Exemple


Volume du cône entre z=0 et z=1:

$V = \int\int\int_VdV = \int_{0}^{2\pi}[\int_{0}^{\frac{\pi}{2}}(\int_{0}^{\frac{\frac{\pi}{4}}{\frac{\pi}{4}+\phi}}r^2sin\phidr)d\phi]d\theta $

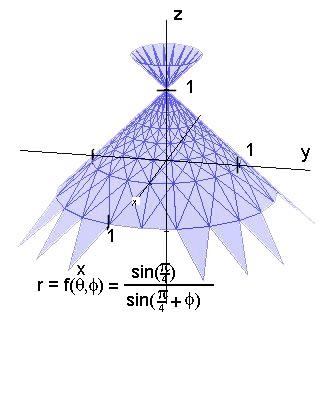
(Ce volume est évidemment plus facile à calculer par coordonnées polaires cylindriques!)