Integrales multiples

Volumes en coordonnées cylindriques: Exemples de calculs de volumes

1) Calculer le volume du cône de hauteur 1, de rayon 1 et délimité par le plan $z=0$. Justifier la fonction $z=1-r$ donnant la surface de ce cône.

On a (Thalès):
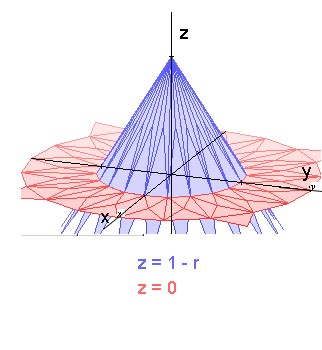
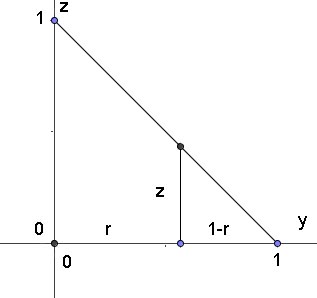
$\frac{z}{1}=\frac{1-r}{1}$
Volume =
$ \int\int_V r dzdrd\theta$
= $ \int_0^{2\pi}[\int_0^1 (\int_0^{1-r}rdz) dr])d\theta$
= $ \int_0^{2\pi}(\int_0^1 r(1-r) dr])d\theta$
= $ \int_0^{2\pi}[\frac{r^2}{2}-\frac{r^3}{3}]_0^1d\theta$
= $\frac{\pi}{3}$

2) Déterminer le volume élimité par le paraboloïde $z=r^2$ et le plan $z=1$

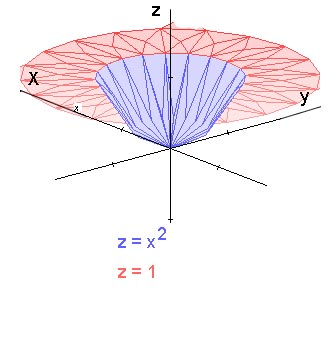
L'intersection des surfaces se fait pour $ r = 1$, d'où:
Volume =
$ \int\int_V r dzdrd\theta$
= $ \int_0^{2\pi}[\int_0^1 (\int_{r^2}^1rdz) dr])d\theta$
= $ \int_0^{2\pi}(\int_0^1 r(1-r^2) dr])d\theta$
= $ \int_0^{2\pi}[\frac{r^2}{2}-\frac{r^4}{4}]_0^1d\theta$
= $\frac{\pi}{2}$

3) Déterminer le volume délimité par les surfaces $z=3-(r-1)^2$ et $z=r$

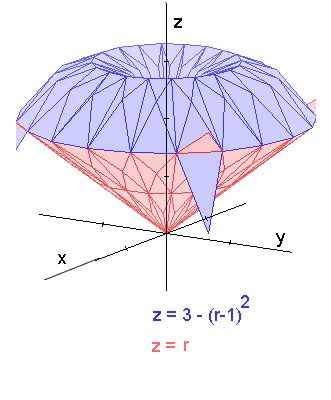
L'intersection des surfaces se fait pour $ r = 1$, d'où:
Volume =
$ \int\int_V r dzdrd\theta$
= $ \int_0^{2\pi}[\int_0^1 (\int_{r}^{3-(r-1)^2}rdz) dr])d\theta$
= $\frac{13\pi}{6}$

4) Calculer le volume du solide cylindrique représenté

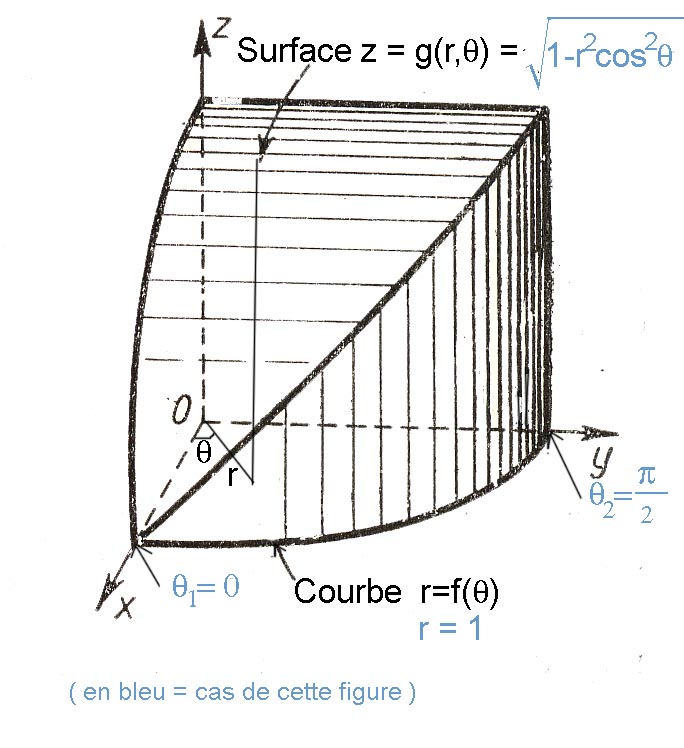
Volume =
$ \int\int_V r dzdrd\theta$
= $ \int_0^{\frac{\pi}{2}}[\int_0^1 (\int_{r}^{\sqrt{1-r^2cos^2\theta}}rdz) dr])d\theta$
= $\frac{3\pi-4}{18}$