Rappel
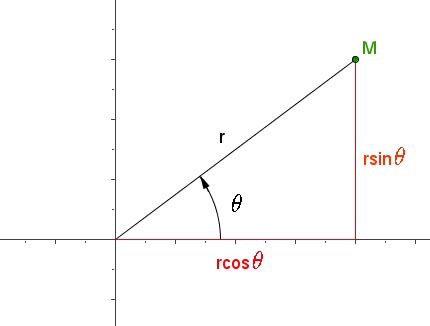
Un point $M(x,y)$ en coordonnées cartésiennes possède les coordonnées polaires $M(r,\theta)$ avec
dS
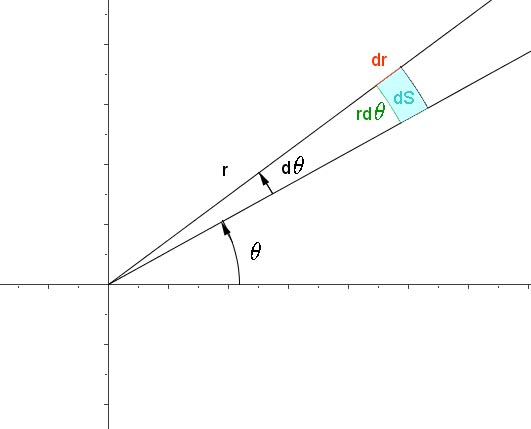
L'élément "infinitésimal" d'aire en coordonnées polaires vaut:
(Pour la compréhension, rappelons que la longueur d'un arc (ici $rd\theta$) vaut le rayon multiplié par l'angle au centre exprimé en radians)
Aires
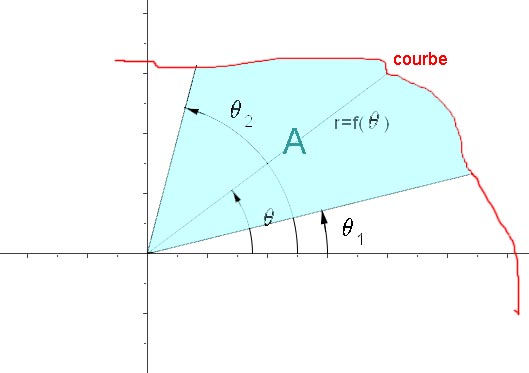
L'équation d'une courbe en coordonnées polaires est souvent réduite à la forme $r = f(\theta)$ et l'aire déterminée par la courbe et un rayon centré sur l'origine et balayant l'angle de $\theta1$ à $\theta2$ est calculée suivant:
(Voir les exemples)