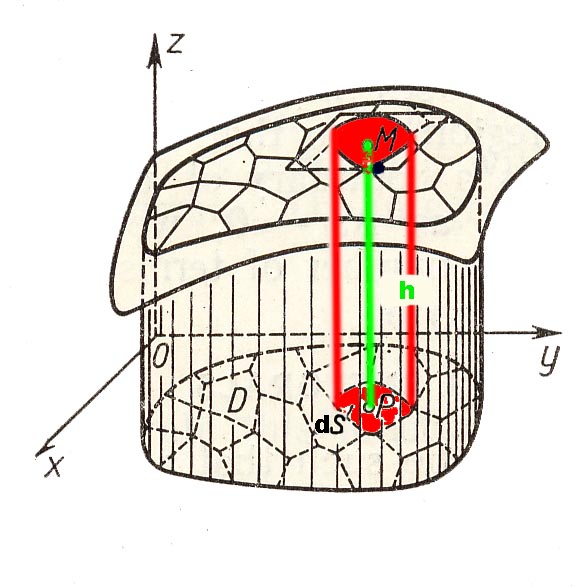
Le volume à calculer est formé de petits cylindres à bases "infiniment petites" dS, de forme en principe quelconques et de hauteur h: C'est la somme des volumes de ces cylindres.
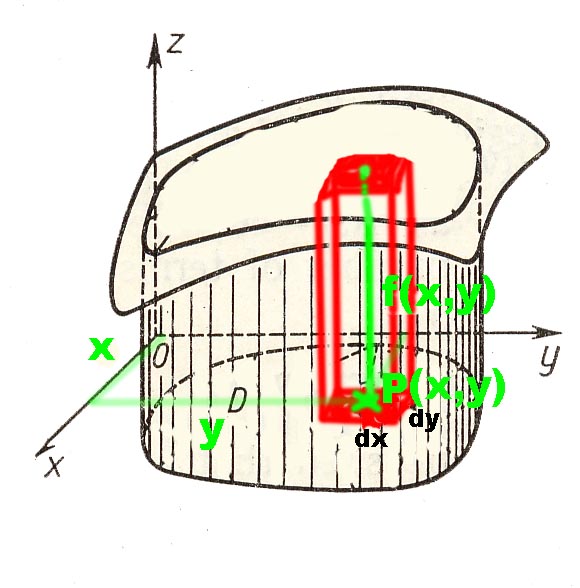
En coordonnées cartésiennes, la base dS est le rectangle infinitésimal d'aire $dxdy$, la hauteur est donnée par la valeur d'une fonction $f$ décrivant la surface supérieure du cylindre prise au point $(x,y)$ , donc $f(x,y)$.
Le volume d'un petit cylindre vaut donc $f(x,y)dxdy$ et le volume entier est la somme des volumes de tous ces petits cylindres qui s'appuient sur le domaine D et qu'on notera:
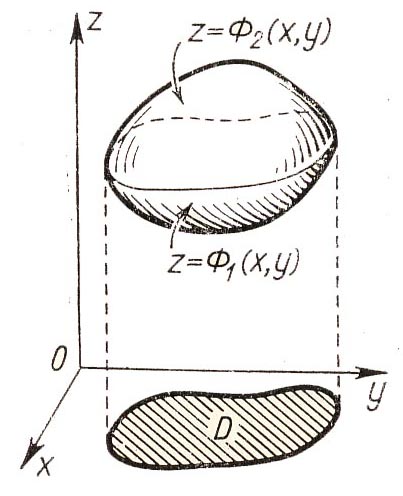
Dans un cas plus général, un volume peut être considéré comme différence de deux volumes cylindriques qu'on notera: