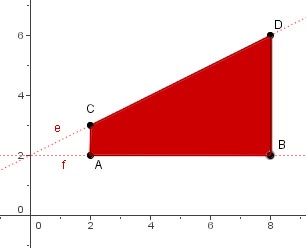
(e): $y=2$
(f): $y=\frac{x}{2}+2$
Aire =
$ \int_2^8(\int_2^{\frac{x}{2}+2}dy)dx$
= $ \int_2^8(\frac{x}{2})dx$
= $ 15$
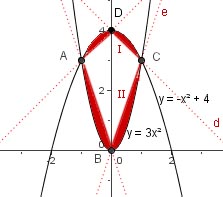
Nous calculons séparément les aires des domaines réguliers I et II:
Points A et C: Intersection des courbes $y=3x^2$ et $y=-x^2+4$; on trouve A(-1,3); C(1,3)
(e): $y=3x$
(f): $y=-x+4$
Aire de I =
$ \int_0^1(\int_{-x+4}^{-x^2+4}dy)dx = \frac{1}{6}$
Aire de II =
$ \int_0^1(\int_{3x^2}^{3x}dy)dx = \frac{1}{2}$
Aire rouge (par raison de symétrie) = $2(\frac{1}{2}+\frac{1}{6})=\frac{4}{3}$
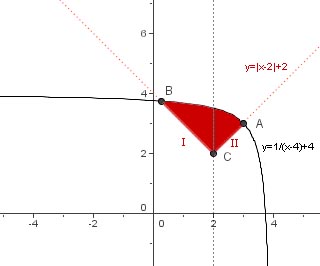
Point A : Intersection des courbes $y=\frac{1}{x-4}+4$ et $y=(x-2)+2 = x$; on trouve $A(3,3)$
Point B : Intersection des courbes $y=\frac{1}{x-4}+4$ et $y=-(x-2)+2 = -x+4$; on trouve $B(2-\sqrt{3},2+\sqrt{3})$
Aire de I =
$ \int_{2-\sqrt{3}}^2(\int_{-x+4}^{\frac{1}{x-4}+4}dy)dx = ln(-2(\sqrt{3}-2))+2\sqrt{3}-\frac{3}{2}$
Aire de II =
$ \int_2^3(\int_x^{\frac{1}{x-4}+4}dy)dx = \frac{3}{2}-ln2$
Aire rouge = $ln(-2(\sqrt{3}-2))+2\sqrt{3}-ln2 = ln(2-\sqrt{3})+2\sqrt{3}$