
Le domaine D est régulier dans la direction de l'axe (Oy), si chaque droite parallèle à (Oy) ne coupe ses limites qu'en deux points (ici $N_1$ et $N_2$). Le domaine représenté est d'ailleurs régulier dans a direction de l'axe (Oy) et aussi (Ox).
puisque pour chaque x variant entre a et b, y varie de $\phi_1(x)$ à $\phi_2(x)$
Si le domaine n'est pas régulier, on le divise en parties régulières, dont on calcule l'aire séparément, par exemple:
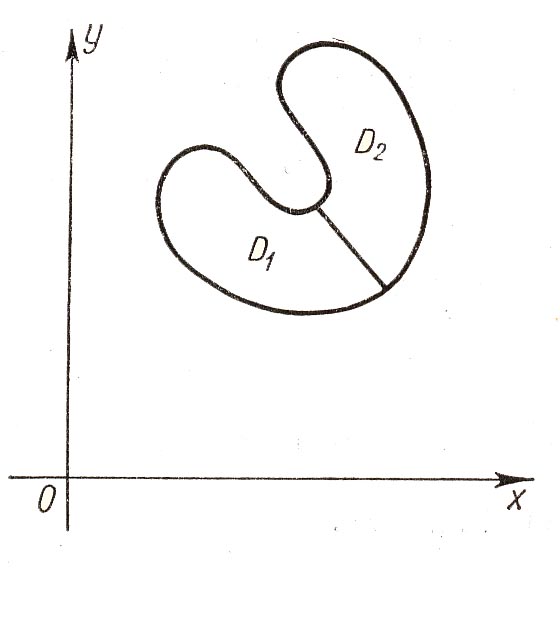
Si une des deux fonctions $\phi_1$ ou $\phi_2$, est définie par morceaux, on coupe de nouveau le domaine en morceaux pour cherher les aires séparément, par exemple:
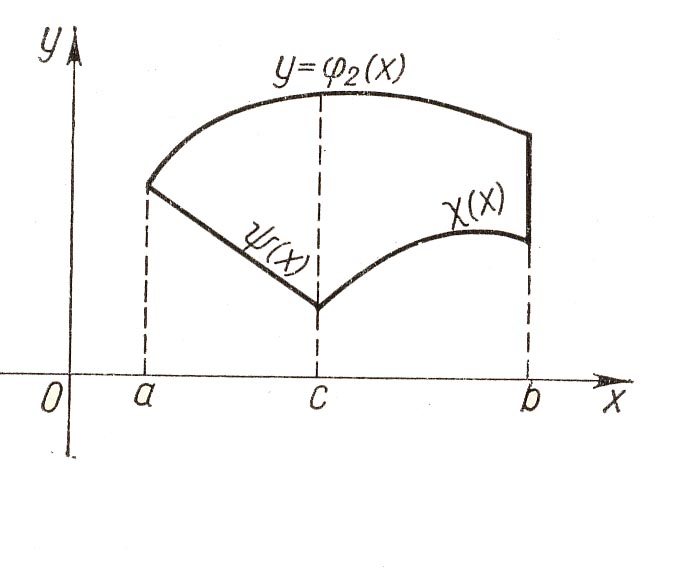
Ici, $\phi_1(x)=\psi(x)$, pour x entre a et c, $\phi_1(x)=\chi(x)$, pour x entre c et b, l'aire du domaine entier sera donc calculée suivant: