

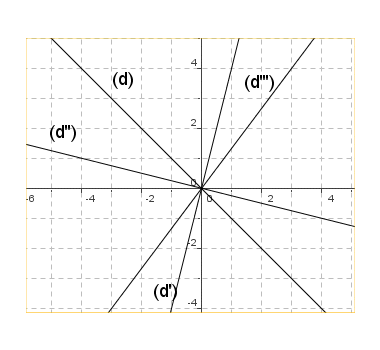
Donner la pente, l’ordonnée à l’origine et l’équation de chacune des droites représentées. |
|
|||||||||||||||
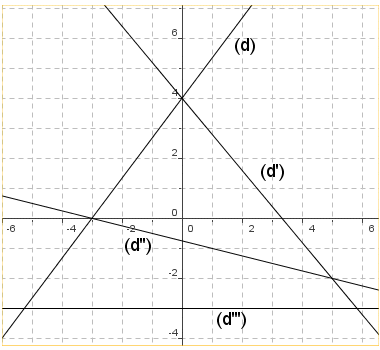
Donner la pente, l’ordonnée à l’origine et l’équation de chacune des droites représentées. |

|
|||||||||||||||
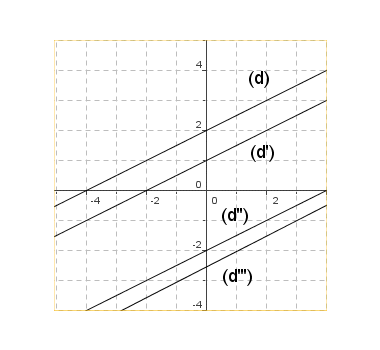
Donner la pente, l’ordonnée à l’origine et l’équation de chacune des droites représentées. |

|
|||||||||||||||

À l’aide d’un graphique, trouver l’équation de la droite qui passe par les points$A(-4,4)$ et B(4,1)) . |
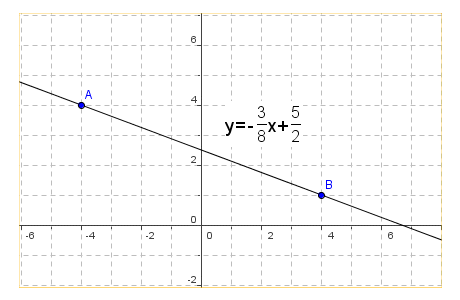
|

à l’aide d’un graphique, trouver l’équation de la droite dont la pente est -$\frac{1}{4}$ et qui passe par le point A(4,0) . |
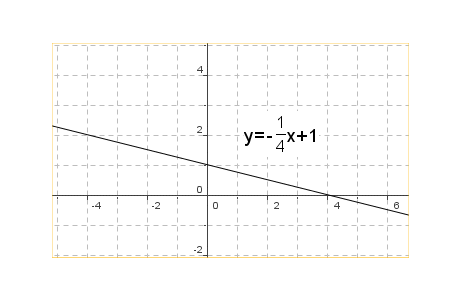
|

Tracer une droite sachant que sa pente est $\frac{2}{3}$ et que son ordonnée à l’origine est -3 . |
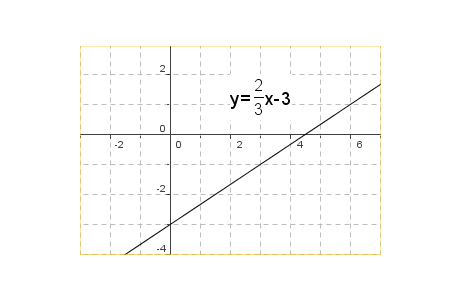
|

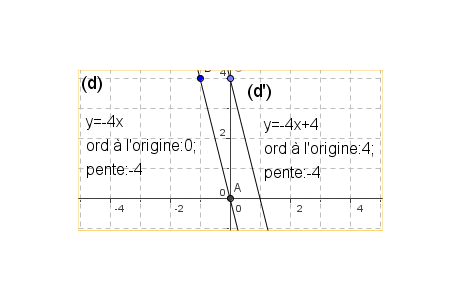
Tracer dans un même système d’axes : la droite d qui passe par les points A(0,0) et B(-2,4) , la droite d' , parallèle à d et passant par le point C(0,4) . Donner la pente, l’ordonnée à l’origine et l’équation de d et de d' . |
|

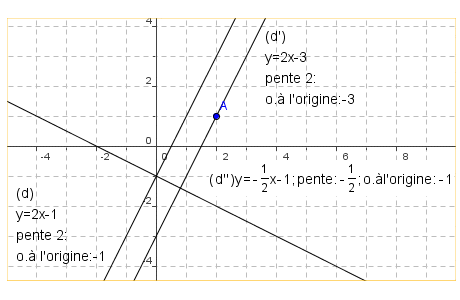
Tracer dans un même système d’axes : la droite d d’équation y=2x-1 , la droite d' , parallèle à d et passant par le point A(2,1) , la droite d'' , perpendiculaire à d et dont l’ordonnée à l’origine est -1 . Donner la pente, l’ordonnée à l’origine et l’équation de d' et de d'' . |
|

Tracer dans un même système d’axes les droites d, d' et d'' , sachant que : d et d' passent par le point A(1,3) , d' et d'' passent par le point B(0,0) , d'' et d passent par le point C(3,2). Donner la pente, l’ordonnée à l’origine et l’équation de chacune des trois droites. |
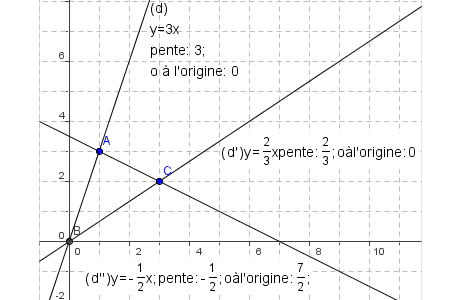
|

|

|