Équations explicites des droites

Pour chaque cas, déterminer deux points de la droite en complétant un tableau
puis tracer la droite dans un repère (O ; $\vec{i}$ ; $\vec{j}$) orthonormal.

(D1) y = 3x + 2
(D2) y = $\frac{4}{3}$x - 1
(D3) y = 3
(D4) x = - 2

Choisissons x et calculons y

Pour D1 : y = 3x + 2

Si x = 0 alors y = 3 x 0 + 2 = 2
Si x = -2 alors y = 3 x (-1) + 2 = -3 + 2 = -1

Pour D2 : y = $\frac{4}{3}$x - 1

Si x = 0 alors y = -1
Si x = 3 alors y = $\frac{4}{3}$ x 3 - 1 = $\frac{12}{3}$ - 1 = 4 - 1 = 3
(on choisira pour x un multiple de 3)

Pour D3 : y = 3

Tous les points ont une ordonnée y égale à 3.
Ex : E(-1 ; 3), F(4 ; 3) ...

Pour D4 : x = -2

Tous les points ont une abscisse x égale à -2.
Ex : G(-2 ; 4) , H(-2 ; -3)

Dans chaque cas, construire la droite d'équation donnée à l'aide
de l'ordonnée à l'origine et du coefficient directeur (pente) :

D1 : y = -4x + 2
D2 : y =-$\frac{5}{3}$x + 3
D3 : y = -5
D4 : x = 4

D1 :
L'ordonnée à l'origine est b = 2 ; la droite passe par le point (O ; 2)
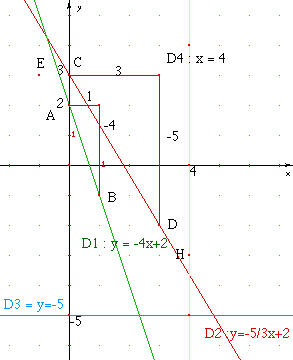
et le coefficient directeur est a = -4

D2 : L'ordonnée à l'origine est b = 3 ; la droite passe par le point (O ; 3)
et le coefficient directeur est a = -$\frac{5}{3}$

D3 : Le coefficient directeur est a = O
D3 est parallèle à l'axe des abscisses
L'ordonnée à l'origine est b = -5

D4 : La droite est parallèle à l'axe des odonnées.

L'équation d'une droite peut s'écrire sous la forme y = ax + b.

Transformer les équations suivantes sous la forme explicite y = ax + b

1° 6x + 6y = 2
2° -4x - 2y = -8
3° 4x - 3y = 9

Isolons y dans chaque égalité

1° 6x + 6y = 2
6y = -6x+2
y=$\frac{-6x+2}{6}$
y=-6$\frac{x}{6}$ + $\frac{2}{6}$
y=-x+1/3

2° -4x - 2y = -8
-2y = 4x - 8
y = -2x + 4

3° 4x - 3y = 9
-3y = -4x + 9
y = $\frac{4}{3}$x - 3

1- Soit D1 la droite d'équation y = -2x +3 et D2 la droite d'équation y = 0,5x + 0,5

Construire les droites D1 et D2 dans un même repère orthonormal (O,$\vec{i}$,$\vec{j}$).

2. Résoudre graphiquement (sans calcul) le système :

y = 0,5x + 0,5 (1)

y = -2x + 3 (2)

Expliquer la méthode.

3. Soit D3 la droite d'équation y = $\frac{5}{10}$x - 15

Sans construire D3, a-t-on D1//D3 ? D2//D3 ? D1$\perp$D3 ? D2$\perp$D3?

Justifier.

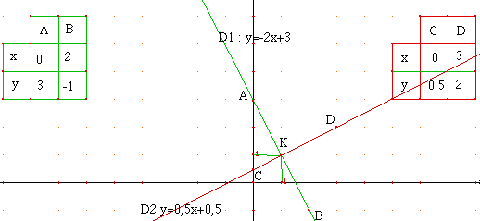
2. Résolvons graphiquement le système :

y = 0,5x + 0,5 (1)

y = -2x + 3 (2)

La représentation graphique de l'équation (1) est la droite D1
De même l'équation (2) est l'équation de la droite D2.

La solution du système représente sur le graphique le couple de coordonnées du point d'intersection de D1 et D2.
Soit K(1 ; 1)

Le système a une seule solution, le couple (1 ; 1)

3. Soit D3 la droite d'équation y = 5/10x - 15,
L'équation de D3 peut se simplifier en y = 0,5x - 15.

Les droites D1 et D3 ont le même coefficient directeur, elles sont donc parallèles.

D'autre part, -2 x 0,5 = -1.

Dans un repère orthonormal, si le produit des coefficients directeurs de deux droites est égal à -1 alors ces droites sont perpendiculaires.

D1 et D2 sont donc perpendiculaires de même que D3 et D2.

Finalement :
D1//D3 ?: oui
D2//D3 ?: non
D1$\perp$D3 ?:non
D2$\perp$D3 ?: oui