Étape 1:
Nous avons ici:
a = 2, l'abscisse pour laquelle nous voulons calculer la dérivée,
x = 5, une abscisse quelconque différente de a ,
en rouge le point A(a, f(a)) ,
en vert le point X(x, f(x)),
en rouge la tangente à la courbe au point A ,
en vert la sécante (AX)
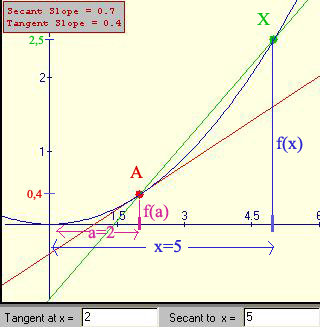
Nous voyons que:
f(x) - f(a) = 2,5 - 0,4 = 2,1
x - a = 5 - 2 = 3
Nous avons ici:
a = 2, l'abscisse pour laquelle nous voulons calculer la dérivée,
x = 5, une abscisse quelconque différente de a ,
en rouge le point A(a, f(a)) ,
en vert le point X(x, f(x)),
en rouge la tangente à la courbe au point A ,
en vert la sécante (AX)

Nous voyons que:
f(x) - f(a) = 2,5 - 0,4 = 2,1
x - a = 5 - 2 = 3
| f(x)-f(a) x-a |
= | 2,1
3 |
= 0,7 |