Démontrer

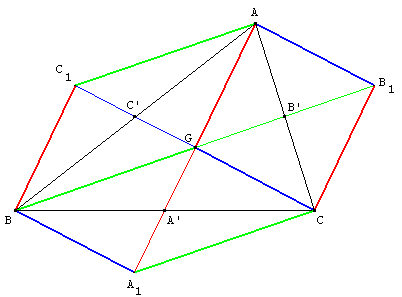
Éléments du triangle quelconque: Centre de gravité.

On donne le triangle (ACB) et les trois médianes (AA'), (BB') et (CC'). (AA') et (BB') se coupent en G. Le but de ce problème est de démontrer que les trois médianes passent par l'unique point G qu'on appelle le centre de gravité du triangle.

1. Compléter par A₁ le parallélogramme (BGCA₁). Démontrer que A₁ est un point de la droite (AA').

2. Compléter par B₁ le parallélogramme (AB₁CG). Démontrer que B₁ est un point de la droite (BB').

3. Démontrer que (AB₁A₁B) est un parallélogramme.

4. Démontrer que G est le milieu de [AA₁] et [BB₁].

5. Compléter par C₁ le parallélogramme (AGBC₁). Démontrer que C₁ est un point de la droite (CB').

6. Démontrer que (ACA₁C₁) est un parallélogramme.

7. Démontrer que G est un point de la droite (CC₁).
   

   → Prérequis → Démonstration par étapes → Démonstration entière