(règle et compas)

Pour construire des droites parallèles ou perpendiculaires à la règle et au compas il faut souvent se ramener à la construction de la médiatrice d'un segment.

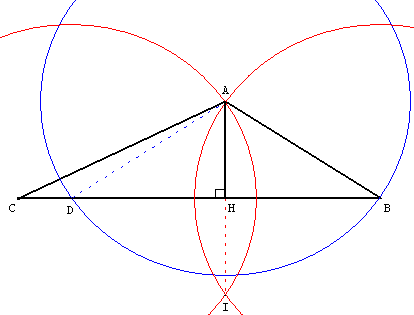Construction d'une hauteur d'un trianglePour trouver, à la règle et au compas, la hauteur relative au côté [BC] d'un triangle ABC tel que AC > AB, construire un triangle isocèle ABD où le point D est l'intersection du cercle de centre A passant par B avec la droite (BC).

Avec les cercles de centres B et D passant par A, tracer la médiatrice (AI) de [BD]. I est le deuxième point d'intersection de ces deux derniers cercles.

La médiatrice (AI) coupe (CD) en H et (AH) est la hauteur cherchée.

 








(test)


Vous pouvez ne cocher aucune ou plusieurs réponses par question.

→ Remplissez s.v.pl. le questionnaire, puis cliquez sur le bouton "score" en bas.



1  ABD est isocèle parce que

  solution   (Attention, si vous cliquez, pas de points pour cette question).

 1        (HA) est orthogonale à (DB)
 2        D et B se trouvent sur un cercle de centre A
 3        DB vaut le double de AB

2  La médiatrice (AH) est aussi hauteur du triangle ABC grāce à une propriété bien connue des médiatrices:

  solution   (Attention, si vous cliquez, pas de points pour cette question).

 1        Tous les points d'une médiatrice sont à la même distance des extrémités du segment
 2        Le pied d'une médiatrice est le milieu du segment de base
 3        Une médiatrice est orthogonale au segment de base

3  On envisage de construire la hauteur en partant d'un cercle de centre A et de rayon AC>AB

  solution   (Attention, si vous cliquez, pas de points pour cette question).

 1        Alors il faut allonger [CB]
 2        C'est impossible
 3        La droite trouvée de cette manière ne sera pas la hauteur cherchée



score  :