Constructions
Test: médiatrice
(règle et compas)
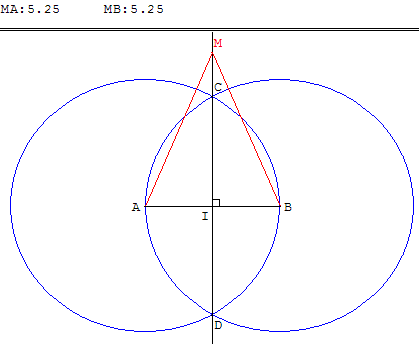 |
Construction d'Œnopide de Chio (Ve siècle avant J.-C.) Dessiner le segment [AB], Cette construction permet de trouver à la règle et au compas le milieu d'un segment. |
(test)
 |
Construction d'Œnopide de Chio (Ve siècle avant J.-C.) Dessiner le segment [AB], Cette construction permet de trouver à la règle et au compas le milieu d'un segment. |