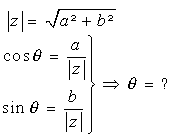Énoncé:
a) Calculer les racines carrées de $z=-\sqrt{3}-i$. Mettre les résultats sous forme algébrique.
b) Mettre $z=-\sqrt{3}-i$ sous forme trigonométrique et en déduire les formes trigonométriques des racines carrées de $z$.
c) En déduire les valeurs exactes du cosinus et sinus de $\frac{7\pi}{12}$.

Prérequis:

  1. Valeurs remarquables des fonctions trigonométriques.
  2. $z=x+iy$ racine de $Z=a+bi$ $\Leftrightarrow$
  3. $z = a+bi$ :
  4. Moivre: $Z=\rho cis(\theta)= \rho(cos\theta+isin\theta)$ et $z^2=Z$ $\Leftrightarrow$ $z=\sqrt{\rho} cis(\frac{\theta}{2})$ ou $z=\sqrt{\rho} cis(\frac{\theta}{2}+\pi)})$.

→ résultats intermédiaires

→ indications

→ résumé de la solution

→ effacer tout

 a)
 $z^2=-\sqrt{3}-i \Leftrightarrow$
(1) $x^2-y^2 =-\sqrt{3}$ et (2) $2xy=-1$ et (3) $x^2+y^2=2$
 Utiliser le prérequis (2e point) pour $Z = -\sqrt{3}-i$.
 (3)+(1): $x=\pm\sqrt{\frac{2-\sqrt{3}}{2}}$
 (3)-(1): $y=\pm\sqrt{\frac{2+\sqrt{3}}{2}}$
 (2): $x$ et $y$ de signes contraires
  d'où:
 $z = \sqrt{\frac{2-\sqrt{3}}{2}}-i\sqrt{\frac{2+\sqrt{3}}{2}}=z_1$  ou
 $z = -\sqrt{\frac{2-\sqrt{3}}{2}}+i\sqrt{\frac{2+\sqrt{3}}{2}}=z_2$
 Résoudre par (3)+(1), puis (3)-(1)
 b)
 $\vert z\vert = \sqrt{3+1}=2$
 $cos\alpha=-\frac{\sqrt{3}}{2}$ et
  $sin\alpha=-\frac{1}{2}$
 $\Leftrightarrow\alpha=-\frac{5\pi}{6} (2\pi)$
 donc: $Z=2cis(-\frac{5\pi}{6})$
 Utiliser le prérequis (3e point) pour $Z = -\sqrt{3}-i$.
 $Z=2 cis(-\frac{5\pi}{12})$ et $z^2=Z$
  $\Leftrightarrow$ $z=\sqrt{2} cis(-\frac{5\pi}{12})=z^'$ ou $z=\sqrt{2} cis(\frac{7\pi}{12})=z^{''}$
 Utiliser le prérequis (5e point) pour $Z = 2cis(-\frac{5\pi}{6})$.
 c)
 $Re(z^{''})=cos(\frac{7\pi}{12})< 0 $ ; $Im(z^{''})=sin(\frac{7\pi}{12})> 0 $
  d'où on déduit que: $z^{''}=z_2
  donc: $cos(\frac{7\pi}{12})=-\frac{\sqrt{2-\sqrt{3}}}{2}$ et $sin(\frac{7\pi}{12})=\frac{\sqrt{2+\sqrt{3}}}{2}$
 Utilisez les signes des parties réelles et imaginaires pour identifier les racines et trouver les réponses.
 Cercle de centre $\Omega(0,\frac{1}{2})$ et de rayon $R=\frac{3}{2}$
 privé du point A(0,-1)
 Est-ce le cercle entier?
 c)
Image
1
h1
1
h1
1
h1